Schubspiegelung (2011/12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Beweis) |
*m.g.* (Diskussion | Beiträge) (→Beweis) |
||
| Zeile 61: | Zeile 61: | ||
::Jede Nacheinanderausführung einer Verschiebung mit einer Geradenspiegelung ist eine Schubspiegelung entsprechend der Definition ''Schubspiegelung''. | ::Jede Nacheinanderausführung einer Verschiebung mit einer Geradenspiegelung ist eine Schubspiegelung entsprechend der Definition ''Schubspiegelung''. | ||
=== Beweis === | === Beweis === | ||
| − | ::Wir gehen aus von der NAF <math>S_g \circ \left( S_b \circ S_a \right)</math> mit <math>a \|| b</math> und <math> g \not{\perp} a</math> | + | ::Wir gehen aus von der NAF <math>S_g \circ \left( S_b \circ S_a \right)</math> mit <math>a \|| b</math> und <math> g \not{\perp} a, g \not{\perp} b</math>. |
{{#ev:youtube|j4T7D4cMN2U}} | {{#ev:youtube|j4T7D4cMN2U}} | ||
[[Kategorie:Elementargeometrie]] | [[Kategorie:Elementargeometrie]] | ||
Version vom 13. Dezember 2011, 13:31 Uhr
Inhaltsverzeichnis |
Die Idee
Entsprechend der Bezeichnung Schubspiegelung würde man unter einer Schubspiegelung dir Nacheinanderausführung Einer Verschiebung mit einer Geradenspiegelung verstehen. Diese Idee ist auch exakt das, was man unter einer Scubspieglung versteht. Trotzdem sie die Definition wie eine Einschränkung dieser Vorstellung aus.
Die Definition
Definition: (Schubspiegelung)
- Es sei
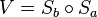eine Geradenspiegelung und 
eine Gerade, die senkrecht auf den Spiegelachsen 
und 
steht. Die NAF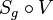 
heißt Schubspiegelung mit der Schubspiegelachse .
- Es sei
Spiegelschiebung?
Entsprechend obiger Definition ist die NAF einer Geradenspiegelung und einer Verschiebung kommutativ,falls sie den Bedingungen der Definition Schubspiegelung genügen.
Satz SCH/1
- Es sei 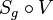eine Schubspieglung. Dann gilt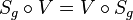
- Es sei
Beweis
- Es sei
.
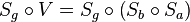- Die Geraden
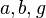haben damit die folgenden Eigenschaften.
- Es sei
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) |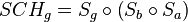 
|
die gegebene Schubspiegelung als NAF dreier Geradenspiegelungen |
| (II) |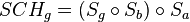 
|
(I), Assoziativität der NAF von Abbildungen |
| (III) |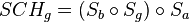 
|
(II), 3. |
| (IV) |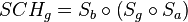 
|
(III), Assoziativität der NAF von Abbildungen |
| (V) |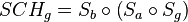 
|
(IV), 2. |
| (VI) |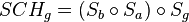 
|
(VI), Assoziativität der NAF von Abbildungen |
| (VII) |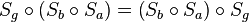 
|
(I), (VI) |
Nach dem Beweis von Satz SCH/1 ist klar, dass die Einschränkung in der Definition Schubspiegelung sinnvoll ist, weil durch diese Einschränkung die Kommutativität der NAF von Geradenspiegelung und Verschiebung gewährleistet ist.
Im folgenden zeigen wir dass die Einschränkung in der Definition des Begriffs Schubspieglung letztlich nicht die Menge aller Schubspiegelungen einschränkt.
Satz SCH/2
- Jede Nacheinanderausführung einer Verschiebung mit einer Geradenspiegelung ist eine Schubspiegelung entsprechend der Definition Schubspiegelung.
Beweis
- Wir gehen aus von der NAF
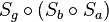mit 
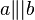und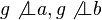 
.
- Wir gehen aus von der NAF
