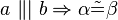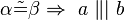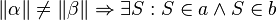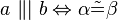Lösung von Aufgabe 2.4 (SoSe 12 P): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> | a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> | ||
| − | b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine dritte Gerade ''c'' jeweils in genau einem Punkt ''S'' geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel <math>\alpha </math> und <math>\beta </math>. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz | + | b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine dritte Gerade ''c'' jeweils in genau einem Punkt ''S'' geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel <math>\alpha </math> und <math>\beta </math>. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äquivalente Aussage (Begründen Sie jeweils)?<br /> |
#<math>\ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta </math> | #<math>\ a \ \|| \ b \Rightarrow \alpha \tilde {=} \beta </math> | ||
#<math>\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b </math> | #<math>\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b </math> | ||
| Zeile 32: | Zeile 32: | ||
da 1. (der satz) und 2. (seine umkehrung) wahr sind,<br /> | da 1. (der satz) und 2. (seine umkehrung) wahr sind,<br /> | ||
kann man formal schreiben: <math>\ A \Leftrightarrow B</math><br /> | kann man formal schreiben: <math>\ A \Leftrightarrow B</math><br /> | ||
| − | kurzfassung:a und b parallel genau dann, wenn stufenwinkel kongruent zueinander.--[[Benutzer:Studentin|Studentin]] 00:29, 25. Apr. 2012 (CEST) | + | kurzfassung:a und b parallel genau dann, wenn stufenwinkel kongruent zueinander.--[[Benutzer:Studentin|Studentin]] 00:29, 25. Apr. 2012 (CEST)<br /> |
| + | Interessante Beiträge, User Studentin! Danke. Frage an alle aus b): Welche der Aussagen sind nun äquivalent?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:18, 28. Apr. 2012 (CEST) | ||
Version vom 28. April 2012, 10:18 Uhr
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt S geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel 
und 
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äquivalente Aussage (Begründen Sie jeweils)?
a)
zwei nichtidentische geraden a und b werden von einer dritten geraden geschnitten.
wenn die geraden a und b parallel zueinander sind, so sind die dabei entstandenen stufenwinkel Fehler beim Parsen(Lexikalischer Fehler): \alpha \
und Fehler beim Parsen(Lexikalischer Fehler): \beta \
kongruent zueinander.--Studentin 00:29, 25. Apr. 2012 (CEST)
b)
1. ist der stufenwinkelsatz:
formal: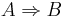 
kurzfassung: wenn a und b parallel, dann stufenwinkel kongruente zueinander--Studentin 00:29, 25. Apr. 2012 (CEST)
2. umkehrung des stufenwinkelsatzes:
formal: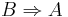
kurzfassung: wenn stufenwinkel kongruent zueinander, dann a und b parallel--Studentin 00:29, 25. Apr. 2012 (CEST)
3. kontraposition:
formal: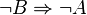 
kurzfassung: wenn stufenwinkel nicht kongruent zueinander, dann existiert ein schnittpunkt (a und b nicht parallel)--Studentin 00:29, 25. Apr. 2012 (CEST)
4.
da 1. (der satz) und 2. (seine umkehrung) wahr sind,
kann man formal schreiben: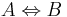 
kurzfassung:a und b parallel genau dann, wenn stufenwinkel kongruent zueinander.--Studentin 00:29, 25. Apr. 2012 (CEST)
Interessante Beiträge, User Studentin! Danke. Frage an alle aus b): Welche der Aussagen sind nun äquivalent?--Tutorin Anne 11:18, 28. Apr. 2012 (CEST)
