Lösung von Aufgabe 3.3 S (SoSe 12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Bemerkungen zu Lösungsvorschlag 2 von M.G.) |
*m.g.* (Diskussion | Beiträge) (→Bemerkungen zu Lösungsvorschlag 2 von M.G.) |
||
| Zeile 33: | Zeile 33: | ||
==== Bemerkungen zu Lösungsvorschlag 2 von M.G. ==== | ==== Bemerkungen zu Lösungsvorschlag 2 von M.G. ==== | ||
| − | @hauleri Schön, dass Sie den Formalismus der Mengenlehre verwenden wollen. Da könnte passen, da es ja um das Schneiden zweier Punktmengen (Geraden) geht. Beachten Sie jedoch: Ein Implikation verknüpft zwei Aussagen: Wenn Aussage a, dann Aussage b. Aussage a wäre unsere Voraussetzung, Aussage b nennen wir die Behauptung. Ob irgendeine "Formulierung" eine Aussage im Sinne der mathematischen Logik ist, erkennt man daran, dass diese Formulierung entweder wahr oder falsch ist. Sie wenden eine Operation auf zwei Mengen an, und bilden den Durchschnitt dieser beiden Mengen: <math>M_1 \cap M_2</math>. Schön, dass ist sowas wie <math>3 + 4</math>. Da | + | @hauleri Schön, dass Sie den Formalismus der Mengenlehre verwenden wollen. Da könnte passen, da es ja um das Schneiden zweier Punktmengen (Geraden) geht. Beachten Sie jedoch: Ein Implikation verknüpft zwei Aussagen: Wenn Aussage a, dann Aussage b. Aussage a wäre unsere Voraussetzung, Aussage b nennen wir die Behauptung. Ob irgendeine "Formulierung" eine Aussage im Sinne der mathematischen Logik ist, erkennt man daran, dass diese Formulierung entweder wahr oder falsch ist. Sie wenden eine Operation auf zwei Mengen an, und bilden den Durchschnitt dieser beiden Mengen: <math>M_1 \cap M_2</math>. Schön, dass ist sowas wie <math>3 + 4</math>. Da fehlt einfach noch ein wenig für eine Aussage. Z.B. <math>3+4=8</math> (Aussage, die falsch ist) oder <math>3+4=7</math> (wahre Aussage) oder eben <math>M_1 \cap M_2 = \{S\}</math> ...--[[Benutzer:*m.g.*|*m.g.*]] 16:32, 6. Mai 2012 (CEST) |
Version vom 6. Mai 2012, 15:32 Uhr
Inhaltsverzeichnis |
Aufgabe 3.3
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösungsvorschlag 1
a)
Kontraposition 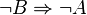
Wenn zwei Geraden nicht nur höchstens einen Punkt gemeinsam haben, dann sind sie identisch.
a) Ich würde vielleicht anstatt "nicht nur höchstens" , "mindestens einen Punkt gemeinsam haben" sagen. Daraus würde ich sagen folgt, dass sie identisch sind oder sich in einem Punkt schneiden, wenn sie wirklich nur einen Punkt dann gemeinsam haben.
b) sehe ich genauso
--Funkdocta 16:23, 6. Mai 2012 (CEST)
b)
Annahme: g und h sind nicht identisch und haben mehr als einen Punkt gemeinsam. --Goliath 16:14, 3. Mai 2012 (CEST)
Lösungsvorschlag 2:
Menge1: g
Menge2: h
Menge1 = Menge 2 oder 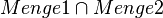 --Hauleri 13:35, 6. Mai 2012 (CEST)
--Hauleri 13:35, 6. Mai 2012 (CEST)
Bemerkungen zu Lösungsvorschlag 2 von M.G.
@hauleri Schön, dass Sie den Formalismus der Mengenlehre verwenden wollen. Da könnte passen, da es ja um das Schneiden zweier Punktmengen (Geraden) geht. Beachten Sie jedoch: Ein Implikation verknüpft zwei Aussagen: Wenn Aussage a, dann Aussage b. Aussage a wäre unsere Voraussetzung, Aussage b nennen wir die Behauptung. Ob irgendeine "Formulierung" eine Aussage im Sinne der mathematischen Logik ist, erkennt man daran, dass diese Formulierung entweder wahr oder falsch ist. Sie wenden eine Operation auf zwei Mengen an, und bilden den Durchschnitt dieser beiden Mengen: 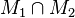 . Schön, dass ist sowas wie
. Schön, dass ist sowas wie 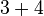 . Da fehlt einfach noch ein wenig für eine Aussage. Z.B.
. Da fehlt einfach noch ein wenig für eine Aussage. Z.B. 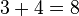 (Aussage, die falsch ist) oder
(Aussage, die falsch ist) oder 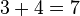 (wahre Aussage) oder eben
(wahre Aussage) oder eben 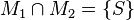 ...--*m.g.* 16:32, 6. Mai 2012 (CEST)
...--*m.g.* 16:32, 6. Mai 2012 (CEST)

