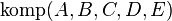Zusatzaufgaben 5 (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 2: | Zeile 2: | ||
Beweisen Sie Satz I.5 : Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen. | Beweisen Sie Satz I.5 : Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen. | ||
| − | [[Lösung von Zusatzaufgabe | + | [[Lösung von Zusatzaufgabe 5.1 (SoSe_12)]] |
| Zeile 8: | Zeile 8: | ||
Beweisen Sie Satz I.7 : Jede Ebene enthält (wenigstens) drei Punkte. | Beweisen Sie Satz I.7 : Jede Ebene enthält (wenigstens) drei Punkte. | ||
| − | [[Lösung von Zusatzaufgabe | + | [[Lösung von Zusatzaufgabe 5.2 (SoSe_12)]] |
| Zeile 20: | Zeile 20: | ||
f) <math>\operatorname{komp}(A, B, C, D, E) </math><br /> | f) <math>\operatorname{komp}(A, B, C, D, E) </math><br /> | ||
| − | [[Lösung von Zusatzaufgabe | + | [[Lösung von Zusatzaufgabe 5.3 (SoSe_12)]] |
Aktuelle Version vom 9. Mai 2012, 12:42 Uhr
Aufgabe 1
Beweisen Sie Satz I.5 : Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Lösung von Zusatzaufgabe 5.1 (SoSe_12)
Aufgabe 2
Beweisen Sie Satz I.7 : Jede Ebene enthält (wenigstens) drei Punkte.
Lösung von Zusatzaufgabe 5.2 (SoSe_12)
Aufgabe 3
Welche Aussagen sind für beliebige Punkte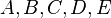 
immer wahr?
a)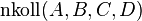 
b)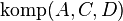 
c)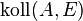 
d)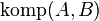 
e)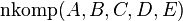 
f) 
