Lösung von Aufgabe 4.6P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
Es sei <math>\ \mathfrak{F}</math> die Menge der Figuren der Ebene. Auf <math>\ \mathfrak{F}</math> sei eine Äquivalenzrelation <math>\ \Theta</math> definiert. <math>\ \Theta</math> möge <math>\ \mathfrak{F}</math> derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen: | Es sei <math>\ \mathfrak{F}</math> die Menge der Figuren der Ebene. Auf <math>\ \mathfrak{F}</math> sei eine Äquivalenzrelation <math>\ \Theta</math> definiert. <math>\ \Theta</math> möge <math>\ \mathfrak{F}</math> derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen: | ||
[[Bild:Figur_Aufgabe_5.jpg]]<br /> | [[Bild:Figur_Aufgabe_5.jpg]]<br /> | ||
| − | Geben Sie mögliche Interpretationen der Relation <math>\ \Theta</math> an.<br /> | + | Geben Sie mögliche Interpretationen der Relation <math>\ \Theta</math> an. <br /> |
| + | |||
| + | der gleiche flächenenhalt z.b.--[[Benutzer:Studentin|Studentin]] 01:22, 11. Mai 2012 (CEST)<br /> | ||
| + | |||
| + | alle Elemente liegen in der gleichen Ebene <br /> | ||
| + | alle n-Ecke mit n größer gleich 3<br /> | ||
| + | alle Elemente mit drei Seiten --[[Benutzer:Honeydukes|Honeydukes]] 21:20, 12. Mai 2012 (CEST)<br /> | ||
| + | |||
| + | |||
| + | |||
| − | |||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Version vom 12. Mai 2012, 20:20 Uhr
Es sei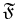 
die Menge der Figuren der Ebene. Auf 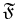sei eine Äquivalenzrelation 
definiert. möge 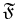derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen:
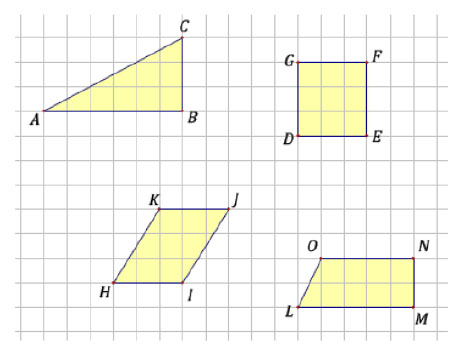
Geben Sie mögliche Interpretationen der Relation an.
der gleiche flächenenhalt z.b.--Studentin 01:22, 11. Mai 2012 (CEST)
alle Elemente liegen in der gleichen Ebene
alle n-Ecke mit n größer gleich 3
alle Elemente mit drei Seiten --Honeydukes 21:20, 12. Mai 2012 (CEST)
