Lösung von Aufgabe 4.6P (SoSe 12)

Es sei $\ \mathfrak{F}$ die Menge der Figuren der Ebene. Auf $\ \mathfrak{F}$ sei eine Äquivalenzrelation $\ \Theta$ definiert. $\ \Theta$ möge $\ \mathfrak{F}$ derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen:
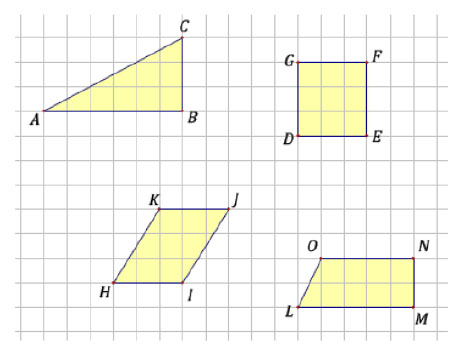
Geben Sie mögliche Interpretationen der Relation $\ \Theta$ an.

der gleiche flächenenhalt z.b.--Studentin 01:22, 11. Mai 2012 (CEST)

alle Elemente liegen in der gleichen Ebene
alle n-Ecke mit n größer gleich 3
alle Elemente mit (mind.) drei Seiten
alle Elemente, deren Flächeninhalt gelb angemalt ist --Honeydukes 21:20, 12. Mai 2012 (CEST)

Honeydukes, das sind gute Ideen für Klassen. Die Aufgabe ist allerdings die Relation zu Interpretieren.
Ein Beispiel: Tim und Jana sind in Klasse 5 und Sina in Klasse 3. - Die math. Klassen sind so "Klasse 5" und "Klasse 3". Die Interpretation der Relation, die zu dieser Klasseneinteilung führt heißt: "gehen in die gleiche Klassenstufe". So gilt: Tim "gehen in die gleiche Klassenstufe" wie Jana. Sie stehen in dieser Relation. Sina und Tim stehen nicht in Relation.
Ich hoffe damit wird klarer, wie die Aufgabe zu verstehen ist.--Tutorin Anne 18:32, 13. Mai 2012 (CEST)

Tetta = "haben den selben Flächeninhalt" oder "haben 3 Ecken" -- Steffem