Diskussion:Lösung von Aufgabe 6: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
|||
| Zeile 3: | Zeile 3: | ||
Ja, in der Tat müssten Sie beweisen, dass ihre Annahme in Schritt 2 korrekt ist. Prima, dass Sie dies erkannt haben! Versuchen Sie den Beweis, er ist nicht schwer!--[[Benutzer:Schnirch|Schnirch]] 16:05, 30. Mai 2010 (UTC) | Ja, in der Tat müssten Sie beweisen, dass ihre Annahme in Schritt 2 korrekt ist. Prima, dass Sie dies erkannt haben! Versuchen Sie den Beweis, er ist nicht schwer!--[[Benutzer:Schnirch|Schnirch]] 16:05, 30. Mai 2010 (UTC) | ||
| + | |||
| + | :: Es gibt zwei Möglichkeiten, mit dem problem umzugehen: | ||
| + | :: Variante 1: man beweist, dass unter der Voraussetzung <math>\operatorname{nKomp} \left( A, B, C, D) \roght)</math> je drei der Punkte <math>\ A, B, C, D</math> nicht kollinear sind. Oder man macht | ||
| + | |||
| + | :: Variante 2: eine Fallunterscheidung | ||
| + | |||
| + | :::Fall: So wie dargestellt | ||
Version vom 2. Juni 2010, 10:05 Uhr
zu 2.
Ich hab unter Schritt (2) vorausgesetzt, dass 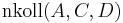 . Ich hab das einfach gemacht, weil ich das Gefühl hatte, dass ich gar nicht weiterkomme bzw. der ganze Beweis keinen Sinn macht, wenn ich nicht das wenigstens voraussetze. Aber ist das überhaupt legitim? --Sternchen 11:13, 21. Mai 2010 (UTC)
. Ich hab das einfach gemacht, weil ich das Gefühl hatte, dass ich gar nicht weiterkomme bzw. der ganze Beweis keinen Sinn macht, wenn ich nicht das wenigstens voraussetze. Aber ist das überhaupt legitim? --Sternchen 11:13, 21. Mai 2010 (UTC)
Ja, in der Tat müssten Sie beweisen, dass ihre Annahme in Schritt 2 korrekt ist. Prima, dass Sie dies erkannt haben! Versuchen Sie den Beweis, er ist nicht schwer!--Schnirch 16:05, 30. Mai 2010 (UTC)
- Es gibt zwei Möglichkeiten, mit dem problem umzugehen:
- Variante 1: man beweist, dass unter der Voraussetzung Fehler beim Parsen(Unbekannte Funktion „\roght“): \operatorname{nKomp} \left( A, B, C, D) \roght)
je drei der Punktenicht kollinear sind. Oder man macht
- Variante 2: eine Fallunterscheidung
- Fall: So wie dargestellt

