Lösung von Zusatzaufgabe 6.2 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
K (Die Seite wurde neu angelegt: „=== Zusatzaufgabe 6.2 === Im Skript steht als Beweis "trivial". Führen Sie die Beweise trotzdem mal durch. Gehen Sie kleinschrittig und gut begründet vor.<br /…“) |
(→Zusatzaufgabe 6.2) |
||
| Zeile 5: | Zeile 5: | ||
a) <math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\operatorname Zw (C, B, A) </math><br /> | a) <math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\operatorname Zw (C, B, A) </math><br /> | ||
b) <math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\operatorname koll (A, B, C) </math><br /> | b) <math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\operatorname koll (A, B, C) </math><br /> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | === Vorschlag Nummero6: === | ||
| + | <br />a)<br /> | ||
| + | '''Voraussetzung: <math>\operatorname(Zw) (A, B, C)</math>'''<br /> | ||
| + | '''Behauptung: <math>\operatorname(Zw) (C, B, A)</math>''' | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !Nr. !!Schritt !! Begründung | ||
| + | |- | ||
| + | | (1) || <math>\operatorname(Zw) (A, B, C)</math> || Voraussetzung | ||
| + | |- | ||
| + | | (2) ||<math>\left| AB \right| + \left| BC \right| = \left| AC \right|</math> || (1), Def.Zwischenrelation | ||
| + | |- | ||
| + | | (3)|| <math>\left| BC \right| + \left| AB \right| = \left| AC \right|</math> || (2), Kommutativgesetz | ||
| + | |- | ||
| + | | (4)|| <math>\left| CB \right| + \left| BA \right| = \left| CA \right|</math> || (3), Axiom II.2 | ||
| + | |- | ||
| + | | (5)|| <math>\operatorname(Zw) (C, B, A)</math> || (4), Axiom II.3 | ||
| + | |} | ||
| + | q.e.d.<br /> | ||
| + | |||
| + | <br />b)<br /> | ||
| + | '''Voraussetzung: <math>\operatorname(Zw) (A, B, C)</math>'''<br /> | ||
| + | '''Behauptung: <math>\operatorname{koll}(A, B, C)</math> ''' | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !Nr. !!Schritt !! Begründung | ||
| + | |- | ||
| + | | (1) || <math>\operatorname(Zw) (A, B, C)</math> || Voraussetzung | ||
| + | |- | ||
| + | | (2) ||<math>\left| AB \right| + \left| BC \right| = \left| AC \right|</math> || (1), Def.Zwischenrelation | ||
| + | |- | ||
| + | | (3)|| <math>\operatorname{koll}(A, B, C)</math> || (2), Axiom II.3 | ||
| + | |} | ||
| + | q.e.d. | ||
| + | |||
| + | --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 08:08, 8. Jun. 2012 (CEST) | ||
| + | |||
| + | |||
| + | |||
| + | |||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Version vom 8. Juni 2012, 07:08 Uhr
Zusatzaufgabe 6.2
Im Skript steht als Beweis "trivial". Führen Sie die Beweise trotzdem mal durch. Gehen Sie kleinschrittig und gut begründet vor.
Beweisen Sie:
a) 

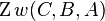
b) 

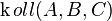
Vorschlag Nummero6:
a)
Voraussetzung: 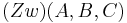
Behauptung: 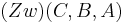
| Nr. | Schritt | Begründung |
|---|---|---|
| (1) | 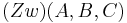 |
Voraussetzung |
| (2) |  |
(1), Def.Zwischenrelation |
| (3) | 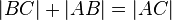 |
(2), Kommutativgesetz |
| (4) | 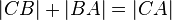 |
(3), Axiom II.2 |
| (5) | 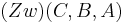 |
(4), Axiom II.3 |
q.e.d.
b)
Voraussetzung: 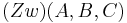
Behauptung: 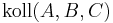
| Nr. | Schritt | Begründung |
|---|---|---|
| (1) | 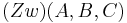 |
Voraussetzung |
| (2) |  |
(1), Def.Zwischenrelation |
| (3) | 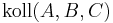 |
(2), Axiom II.3 |
q.e.d.
--Tchu Tcha Tcha 08:08, 8. Jun. 2012 (CEST)

