Lösung von Zusatzaufgabe 6.2 S (SoSe 12)

Zusatzaufgabe 6.2

Im Skript steht als Beweis "trivial". Führen Sie die Beweise trotzdem mal durch. Gehen Sie kleinschrittig und gut begründet vor.
Beweisen Sie:
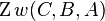
a) $\operatorname Zw (A, B, C)$ $\Rightarrow$ $\operatorname Zw (C, B, A)$
b) $\operatorname Zw (A, B, C)$ $\Rightarrow$ $\operatorname koll (A, B, C)$

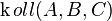
Vorschlag Nummero6/Tchu Tcha Tcha:

a)
Voraussetzung: 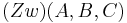$\operatorname(Zw) (A, B, C)$
Behauptung: 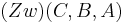$\operatorname(Zw) (C, B, A)$

Nr.	Schritt	Begründung
(1)	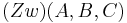$\operatorname(Zw) (A, B, C)$	Voraussetzung
(2)	$\left| AB \right| + \left| BC \right| = \left| AC \right|$	(1), Def.Zwischenrelation
(3)	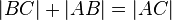$\left| BC \right| + \left| AB \right| = \left| AC \right|$	(2), Kommutativgesetz
(4)	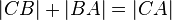$\left| CB \right| + \left| BA \right| = \left| CA \right|$	(3), Axiom II.2
(5)	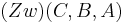$\operatorname(Zw) (C, B, A)$	(4), Axiom II.3

q.e.d.

b)
Voraussetzung: 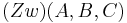$\operatorname(Zw) (A, B, C)$
Behauptung: 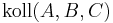$\operatorname{koll}(A, B, C)$

Nr.	Schritt	Begründung
(1)	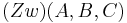$\operatorname(Zw) (A, B, C)$	Voraussetzung
(2)	$\left| AB \right| + \left| BC \right| = \left| AC \right|$	(1), Def.Zwischenrelation
(3)	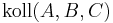$\operatorname{koll}(A, B, C)$	(2), Axiom II.3

q.e.d.

--Tchu Tcha Tcha 08:08, 8. Jun. 2012 (CEST)

Alles korrekt! Super!--Buchner 10:55, 11. Jun. 2012 (CEST)