Lösung von Aufg. 11.2 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 18: | Zeile 18: | ||
NW_1+NW_2= 180 ,und daraus nach Rechnen in R folgt, dass <math>\left| \beta' \right|</math>= <math>\left| \angle ABC \right|</math> = 90 ist,<br /> | NW_1+NW_2= 180 ,und daraus nach Rechnen in R folgt, dass <math>\left| \beta' \right|</math>= <math>\left| \angle ABC \right|</math> = 90 ist,<br /> | ||
kann <math>\left| \beta' \right|</math> nicht größer als <math>\left| \angle BAC \right|</math> sein (,da <math>\left| \angle ABC \right| = \left| \angle BAC \right| = 90</math>) ..<br />Widerspruch zur Annahme. Behauptung stimmt. qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:04, 5. Jul. 2012 (CEST)<br /> | kann <math>\left| \beta' \right|</math> nicht größer als <math>\left| \angle BAC \right|</math> sein (,da <math>\left| \angle ABC \right| = \left| \angle BAC \right| = 90</math>) ..<br />Widerspruch zur Annahme. Behauptung stimmt. qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:04, 5. Jul. 2012 (CEST)<br /> | ||
| − | *Also die Behauptung stimmt so nicht. Ich glaube, dass hier Annahme und Behauptung vertauscht/verwechselt wurde. Der Beweis sollte noch einmal überarbeitet werden, da du eigentlich zu keinem Widerspruch zur Annahme, sondern zu einem Widerspruch zum schwachen Außenwinkelsatz kommst.--[[Benutzer:Andreas|Tutor Andreas]] 11:11, 10. Jul. 2012 (CEST) | + | *Also die Behauptung stimmt so nicht. Ich glaube, dass hier Annahme und Behauptung vertauscht/verwechselt wurde. Der Beweis sollte noch einmal überarbeitet werden, da du eigentlich zu keinem Widerspruch zur Annahme, sondern zu einem Widerspruch zum schwachen Außenwinkelsatz kommst.--[[Benutzer:Andreas|Tutor Andreas]] 11:11, 10. Jul. 2012 (CEST)<br />Ja stimmt.--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:15, 10. Jul. 2012 (CEST) |
[[Kategorie:Einführung_S]]<br/> | [[Kategorie:Einführung_S]]<br/> | ||
<br/> | <br/> | ||
Version vom 10. Juli 2012, 12:15 Uhr
Aufgabe 11.2
Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Lösungsversuch Nummero6/Tchu Tcha Tcha:
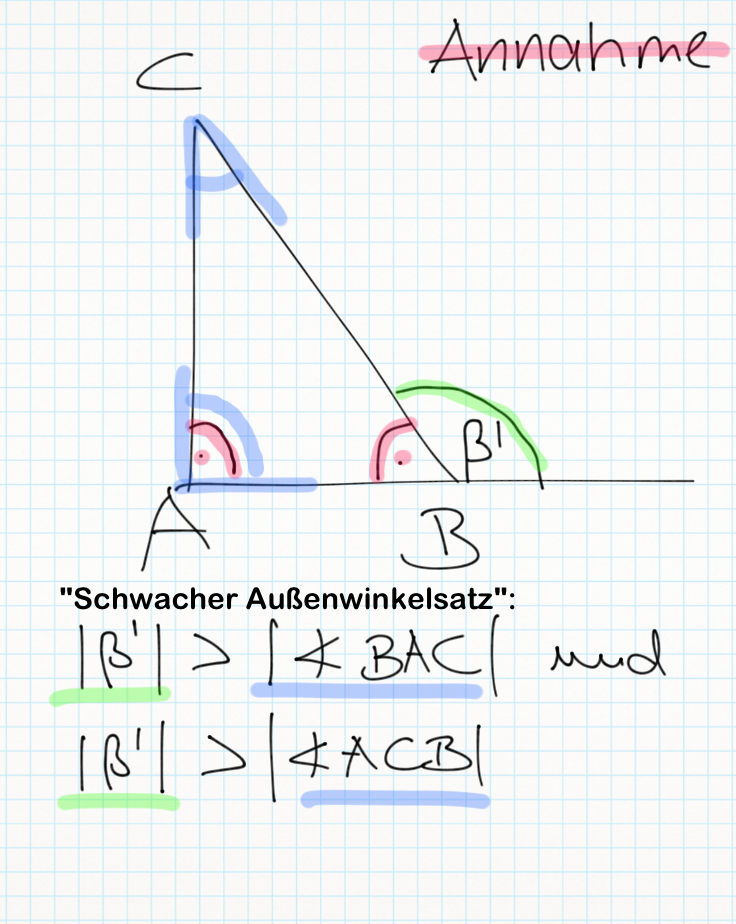
Voraussetzung: Dreieck (
)
Annahme: mindestens 2 Innenwinkel sind spitze Winkel (Größe: kleiner 90)
Behauptung: genau 1 Innenwinkel ist ein spitzer Winkel
oBdA.: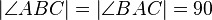 
Nach dem "Schwachen Außenwinkelsatz" gilt:
.
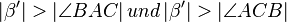Da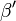 
der NW von 
ist und nach dem Supplementaxiom und Def supplementär gilt:
NW_1+NW_2= 180 ,und daraus nach Rechnen in R folgt, dass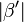 
= 
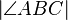= 90 ist,
kann 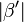nicht größer als 
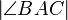sein (,da ) ..
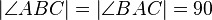Widerspruch zur Annahme. Behauptung stimmt. qed
--Tchu Tcha Tcha 13:04, 5. Jul. 2012 (CEST)
- Also die Behauptung stimmt so nicht. Ich glaube, dass hier Annahme und Behauptung vertauscht/verwechselt wurde. Der Beweis sollte noch einmal überarbeitet werden, da du eigentlich zu keinem Widerspruch zur Annahme, sondern zu einem Widerspruch zum schwachen Außenwinkelsatz kommst.--Tutor Andreas 11:11, 10. Jul. 2012 (CEST)
Ja stimmt.--Tchu Tcha Tcha 13:15, 10. Jul. 2012 (CEST)
Weitere Lösung:
<document>RitterSport_IMG_0001.pdf</document>
--RitterSport 13:13, 10. Jul. 2012 (CEST)
