Lösung von Zusatzaufgabe 8.2 S: Unterschied zwischen den Versionen

Version vom 17. Juli 2012, 21:49 Uhr

Lösungsversuch Nummero6/Tchu Tcha Tcha:
Def. (Inneres eines Kreises):
Es sei K ein Kreis mit Mittelpunkt M und Radius r in einer Ebene E.
Die Menge aller Punkte 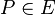, für die gilt: 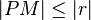nennt man Inneres eines Kreises.
--Tchu Tcha Tcha 09:56, 16. Jun. 2012 (CEST)
Passt! --Tutor Andreas 12:11, 12. Jul. 2012 (CEST)

Ist für das Innere des Kreises 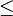richtig oder müsste es nicht < r sein? gehört der "Rand" mit zum Inneren?
--Thommy 21:57, 17. Jul. 2012 (CEST)

Wie würden Sie sich entscheiden? Würden Sie den Rand mit dazu nehmen oder nicht? Wenn Sie den Rand nicht dabei haben wollten und sagen würden, das eine ist das Innere und das andere die Figur selbst also bitte halten wir das dann auch auseinander, hätte das doch eine gewisse Logik. Der Dozent könnte nun sagen, dass er es persönlich gern so hätte (vielleicht weil er selbst unsicher ist, nichts ist schlimmer als unsichere Lehrer), dass der Rand mit dabei ist und er das in der Klausur auch gern so hören würde. Ein solcher Dozent sollte seinen Job an den Nagel hängen und Currywürste verkaufen (wenn er das denn könnte). Ich glaube schon, dass Sie verstehen, dass es bei der einen oder anderen Beweisführung mitunter einfacher wäre, wenn der Rand beim Inneren mit dabei ist oder auch nicht. Nehmen wir das Innere eine Winkels. Für die diversen Lemmata aus dem Inneren von Winkeln schreiben sich die Beweise mitunter einfacher, wenn wir den Winkel selbst mit zu seinem Inneren zählen. Man könnte sie aber auch führen, wenn der Winkel nicht mit dazu gehört, könnte teilweise zu Fallunterscheidungen führen, auf die keiner Lust hat. Bei den Strecken haben wir die offene und die Strecke selbst. Wir könnten auch vom offenen Inneren und vom geschlossenen Inneren des Kreises sprechen. Die Mathematik würde sich nicht großartig ändern. Lange Rede, kurzer Sinn, lassen Sie sich durch derartige Dinge nicht verunsichern. Würden Sie in der Klausur als Inneres nur alle Punkte akzeptieren, deren Abstand zum Mittelpunkt echt kleiner als der Radius des Kreises ist, wäre das korrekt. Ebenso könnte jemand sagen, o.k. den Kreis selbst könnten wir eigentlich mit dazu nehmen, also schreibe ich Abstand des jeweiligen Punktes zum Mittelpunkt des Kreises ist kleiner oder gleich dem Radius. Niemand würde ihm diese Einstellung verwehren können. Das Innere ist konvex, nehmen wir den Rand mit dazu bleibt es konvex. Sie sollten verstehen, dass die Problematik marginal ist. --*m.g.* 22:49, 17. Jul. 2012 (CEST)