Sehnenviereck SS 12: Unterschied zwischen den Versionen
Oz44oz (Diskussion | Beiträge) (→Funktionale Betrachtung) |
Oz44oz (Diskussion | Beiträge) (→Definitionen) |
||
| Zeile 5: | Zeile 5: | ||
| − | + | 1. Es sei <math>\ k</math> ein Kreis. Eine Sehne des Kreises ist jede Strecke, deren Anfangs- und Endpunkte Element des Kreises <math>\ k</math> sind. | |
| − | + | 2. .......... | |
=== Durchmesser=== | === Durchmesser=== | ||
| − | + | 1. Es sei <math>\ k</math> ein Kreis mit dem Mittelpunkt <math>\ M </math>. Ferner seien <math>\ A</math> und <math>\ B </math> zwei Punkte des Kreises <math>\ k</math>. Ein Durchmesser ist die Strecke <math>\overline {AB}</math>, für die gilt <math> \operatorname{Zw} \left( A, M, B\right)\wedge A,B\in \ k</math>. | |
| + | |||
| + | |||
=== Radius === | === Radius === | ||
| − | + | 1. Es sei <math>\ k</math> ein Kreis mit dem Mittelpunkt <math>\ M </math>. Jede Strecke, die den Anfangspunkt in <math>\ M </math> und den Endpunkt in einem beliebigen Punkt des Kreises <math>\ k</math> hat, nennt man Radius. | |
=== Erarbeitung des Begriffs Sehnenviereck === | === Erarbeitung des Begriffs Sehnenviereck === | ||
Version vom 18. Juli 2012, 19:44 Uhr
Inhaltsverzeichnis |
Definitionen
Kreissehne
1. Es sei  ein Kreis. Eine Sehne des Kreises ist jede Strecke, deren Anfangs- und Endpunkte Element des Kreises
ein Kreis. Eine Sehne des Kreises ist jede Strecke, deren Anfangs- und Endpunkte Element des Kreises  sind.
sind.
2. ..........
Durchmesser
1. Es sei  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner seien
. Ferner seien  und
und  zwei Punkte des Kreises
zwei Punkte des Kreises  . Ein Durchmesser ist die Strecke
. Ein Durchmesser ist die Strecke  , für die gilt
, für die gilt 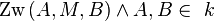 .
.
Radius
1. Es sei  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Jede Strecke, die den Anfangspunkt in
. Jede Strecke, die den Anfangspunkt in  und den Endpunkt in einem beliebigen Punkt des Kreises
und den Endpunkt in einem beliebigen Punkt des Kreises  hat, nennt man Radius.
hat, nennt man Radius.
Erarbeitung des Begriffs Sehnenviereck
Sehnenviereck
Sätze
Satzfindung
sehr speziell: Quadrate
Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.
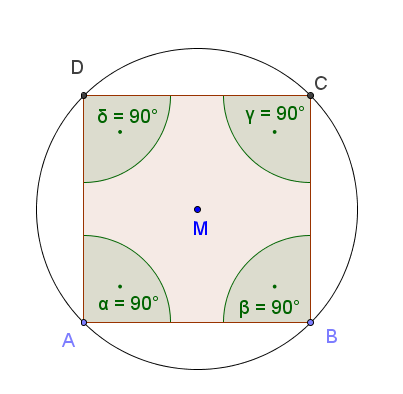
weniger speziell, aber immer noch ziemlich speziell: Rechtecke
Jedes Rechteck ist ein Sehnenviereck.
noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze
Jedes gleichschenklige Trapez ist ein Sehnenviereck.
allgemeines Sehnenviereck
Ausgangslage: 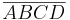 ist ein gleichschenkliges Trapez.
ist ein gleichschenkliges Trapez.
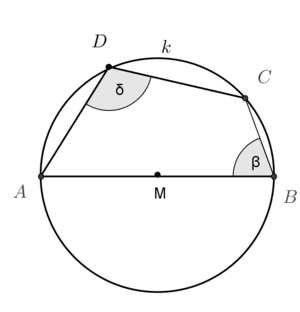
Arbeitsauftrag: Bewegen Sie den Punkt  auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von
auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von 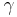 ? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?
? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?
Der Satz über die gegenüberliegenden Winkel im Sehnenviereck
Satz 1
In jedem Sehnenviereck sind die gegenüberliegenden Winkel supplementär.
--Oz44oz 20:32, 18. Jul. 2012 (CEST)Satz 2 : Die Umkehrung vom Satz 1
Kriterium
Beweise
wir wissen
--Oz44oz 22:55, 17. Jul. 2012 (CEST)
zu zeigen:
--Oz44oz 23:03, 17. Jul. 2012 (CEST)
Beweis vom Satz 1
| Beweis 1 | Beweis 2 | Beweis 3 |
|---|---|---|
 |
 |

|
Beweisen Sie 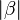 + +  = 180 = 180 |
Beweisen Sie 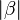 + +  = 180 = 180 |
Beweisen Sie 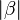 + +  = 180 = 180
|
--Oz44oz 19:19, 16. Jul. 2012 (CEST)
Voraussetzung:
Behauptung:
Beweis 1:
Beweis vom Satz 2
| Beweis 1 | Beweis 2 |
|---|---|
 |

|
| Beweisen Sie..... | Beweisen Sie........ |
--Oz44oz 19:15, 16. Jul. 2012 (CEST)
Voraussetzung:
Behauptung:
Annahme:
Beweis 1:
Funktionale Betrachtung
--Oz44oz 22:47, 16. Jul. 2012 (CEST)
--Oz44oz 22:45, 17. Jul. 2012 (CEST)


