Fixpunkt, Fixpunktgerade, Fixgerade (2012 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition 3.1: (Fixpunkt einer Abbildung \ \phi ))
(→‎Richtig verstanden?)
Zeile 27: Zeile 27:
 
+ (c) Es sei <math>\ Z</math> der Schnittpunkt der Geraden <math>\ h</math> und <math>\ g</math>. <math>\ Z</math> ist Fixpunkt bezüglich <math>\ S_h \circ S_g</math>.
 
+ (c) Es sei <math>\ Z</math> der Schnittpunkt der Geraden <math>\ h</math> und <math>\ g</math>. <math>\ Z</math> ist Fixpunkt bezüglich <math>\ S_h \circ S_g</math>.
 
+ (d)  Es sei <math>\ Z</math> der Schnittpunkt der Geraden <math>\ h</math> und <math>\ g</math>. <math>\ Z</math> ist Fixpunkt bezüglich <math>\ S_g \circ S_h</math>.
 
+ (d)  Es sei <math>\ Z</math> der Schnittpunkt der Geraden <math>\ h</math> und <math>\ g</math>. <math>\ Z</math> ist Fixpunkt bezüglich <math>\ S_g \circ S_h</math>.
−
- (e) Jede Drehung hat genau einen Fixpunkt.
+
- (e) Jede von der Identität verschiedene Drehung hat genau einen Fixpunkt.
 
- (f) Es gibt fixpunktfreie Geradenspiegelungen.
 
- (f) Es gibt fixpunktfreie Geradenspiegelungen.
 
+ (g) Es gibt fixpunktfreie Verschiebungen.
 
+ (g) Es gibt fixpunktfreie Verschiebungen.
Zeile 33: Zeile 33:
  
 
</quiz>
 
</quiz>
−
[[Diskussion zum Quiz]]
 
  
 
== Fixgeraden ==
 
== Fixgeraden ==

Version vom 5. November 2012, 16:52 Uhr

Inhaltsverzeichnis

Fixpunkte

Beispiele/Gegenbeispiele

1. In welchen Fällen handelt es sich um Fixpunkte bezüglich der genannten Abbildung?

(a) Punkt \ A auf der Geraden \ g bezüglich der Spiegelung an \ g.
(b) Punkt \ A auf der Geraden \ g bezüglich einer Verschiebung längs \ g.
(c) Punkt \ Z bezüglich einer Drehung mit dem Drehwinkel \alpha = 30^\circ um \ Z.
(d) Punkt \ Z bezüglich einer Drehung mit dem Drehwinkel \alpha = 360^\circ um \ Z.
(e) Punkt A \notin g bezüglich der Spiegelung an \ g.
(f) Jeder Punkt \ Q bezüglich der Identität.
(g) Jeder Punkt \ D bezüglich einer zentrischen Streckung an dem Punkt \ Z.
(h) Der Punkt \ D bezüglich einer zentrischen Streckung an sich selbst.
(i) Jeder Punkt der Ebene \ \delta bezüglich einer senkrechten Parallelprojektion auf die Ebene \ \delta.
(j) Der Zentralpunkt \ Z einer Zentralprojektion.

Punkte: 0 / 0


Definition des Begriffs Fixpunkt einer Abbildung

Definition 3.1: (Fixpunkt einer Abbildung 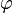\ \varphi )
Ein Punkt 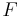\ F heißt Fixpunkt einer Abbildung 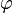\ \varphi, wenn 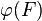\varphi (F) auf F abgebildet wird.

Richtig verstanden?

1. Kennzeichnen Sie die wahren Aussagen

(a) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_h.
(b) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_g.
(c) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_h \circ S_g.
(d) Es sei \ Z der Schnittpunkt der Geraden \ h und \ g. \ Z ist Fixpunkt bezüglich \ S_g \circ S_h.
(e) Jede von der Identität verschiedene Drehung hat genau einen Fixpunkt.
(f) Es gibt fixpunktfreie Geradenspiegelungen.
(g) Es gibt fixpunktfreie Verschiebungen.
(h) Ihr Beispiel ... .

Punkte: 0 / 0


Fixgeraden

Beispiele/Gegenbeispiele

Definition

  • Eine Gerade g, die bei der Abbildung \phi auf sich selbst abgebildet wird, ist eine Fixgerade.


--Flo60 22:19, 9. Nov. 2011 (CET)

--Flo60 15:03, 10. Nov. 2011 (CET)

Richtig verstanden?

Fixpunktgeraden

Beispiele/Gegenbeispiele

Definition

  • Eine Fixgerade f einer Abbildung \phi ist genau dann eine Fixpunktgerade bzgl. der Abbildung \phi, wenn gilt: 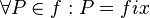\forall P \in f: P = fix--Flo60 22:22, 9. Nov. 2011 (CET)

Richtig verstanden?

1. Kennzeichnen Sie die wahren Aussagen

(a) Manche Fixpunktgeraden einer Abbildung sind Fixgeraden derselben Abbildung.
(b) Jede Fixpunktgerade einer Abbildung ist eine Fixgerade dieser Abbildung.
(c) Jede Fixgerade einer Abbildung ist eine Fixpunktgerade dieser Abbildung.
(d) g sei Fixpunktgerade der Bewegung \phi, dann gilt: \forall P \in g . P = \phi (P) --~~~~
(e) weitere Beispiele ... .

Punkte: 0 / 0

und wieder Diskussion

Von „http://geometrie.zum.de/index.php?title=Fixpunkt,_Fixpunktgerade,_Fixgerade_(2012_13)&oldid=18320“