Serie 03 12 13: Unterschied zwischen den Versionen
Jessy* (Diskussion | Beiträge) (→Aufgabe 3.1) |
Jessy* (Diskussion | Beiträge) (→Aufgabe 3.1) |
||
| Zeile 8: | Zeile 8: | ||
<ggb_applet width="603" height="627" version="4.0" ggbBase64="UEsDBBQACAAIALyObkEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAC8jm5BAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVabW/bthb+3P0KQhj24aK2+SZS6pwOSYDhFk3XosmG4X4ZaIl2uMiSJ8mOU+zH30NSkmU7cZM6d+0N4pAiD3l4znnOC+WMf1rPM7TSZWWK/CQgQxwgnSdFavLZSbCsp4Mo+On1d+OZLmZ6Uio0Lcq5qk8CbilNehJMNOaCRXSgYzEZ8KlMBxOC5YCohGOpxESSKEBoXZlXefGLmutqoRJ9mVzrubooElU7xtd1vXg1Gt3e3g5bVsOinI1ms8lwXaUBgmPm1UnQdF7BdluLbpkjpxiT0e/vLvz2A5NXtcoTHSArwtK8/u7F+NbkaXGLbk1aX58EgsQButZmdg0yyQhkGlmiBShkoZParHQFS3uPTuZ6vggcmcrt/AvfQ1knToBSszKpLk8CPJSUSS7jCAvCopixABWl0Xnd0JKG56jdbbwy+tZva3uOIw9QXRTZRNkd0d9/I4opRi9tQ3xDoRHCT2E/hplvqG+4b0JPw/1y7km5p+GehsMZV6Yyk0yfBFOVVaBBk09LsF73XNV3mXbnaQY20pOXIFNlPgExw6BSr3IYx/il/Qj4cNzouick6XGty+UTmbYsBWaPZ0mPEpS1PDmP9nnS8AExxQGmXu7HyEnCnmqBlft1nz2O7JCYuxz983EMBf9HRByPWlcZN96BqmtL26Cn1vPK+guLURhb2BMUgm8ICSgPEYmhkRSBNyASIh7CI4mQsK1ETMIERwxFyNIRhpxzhBH84dJtJlAIm9lRCT6JCDDiKGSIOJ/iCDwJOb8EH6UMKMIQhbDIsifUbsEE4gKeWIQ4nNG6pCRAyGAhPAN7ihhBzC4mElGBhN2PcOvqIrJHhy0pEhgJYjcErwaP9t4M9BFiVhrRqMvki2W9paJknrbdulh0tgBqiEebqOfj01ZQfDHO1ERnkCcurSURWqnMeoRjNC3yGjVGpNiPzUq1uDZJdanrGlZV6E+1Uheq1uufgbpqeTvapMirD2VRnxfZcp5XCCVFhrszFxnp9Wl3anhgvQnenwh7E6LXl/fyLWAGLSsN/IuyaslVmr6xFJvQAJp8n2d3Z6VWN4vCbIsxHrmUM9bLJDOpUflvAFbLxeoFdRnIhqs2A4Vx3B6kKNPLuwoQjNb/0WUBeozkUAiCRUQ4IxENA3TnZyDIDjkmEvKLIELEEk6WKOt6VMghpiGnhHKGJXC6e2AGtnOM9aqzj1rrTvRZad26Eds+vKnOimwz5IQ/V4t6WbrKATiVVqTTfJZpBxAXayEtJzeTYn3p3Zv5va7uFvDUwGQyc0pHEBhoCDLOmnbiW0djT9ZRYUeDHUUHNZN28ySmjsK1E986KsCuP1ojKWnFJLhlYyoXznCw5TQO+DbJL3NTX7QPtUluGkmJp/9lOZ/oDj7bW5Jn2nI82oHX+EaXuc4aNIMll8Wy8s7ZA3qqEzOHRz/RKERZY/0KB/CjqZ6Vuj135moyry43i/tA3Rt2W/1cFvM3+eoKkLBzgPGoPeW4SkqzsIBDE8gAN3qDqdRUChJI2l9n3Q9ET2yiAPXUVjXgmMv6ugBTz4ezIayDmAKj1vMyPYdCC9UOYA6jnarfuQrO6hQVkz8hrO2YYmMzmH4AbEhli2tla7xG7Ezd6XJLEW63d0Wqt+KjykH7Tgbw8IXdwNp3obVHhj8vdBawofOnrRgFGq/Q2rNFd037yVfvvny1klof22LqR/ctCF5rT+LGvn/3fYMqr7o9JebLuS5N0qnpo1MjrF02u3aH2FJtm+P9op40j1EueaRyyf3KvUe1+D7V9oVOivlc5SnKXcVybsok08EmhSpsAYQUsQrwcizrduKt36zZYk+DAOGe/t5+TRhuImANmfkGrh+VC9Odkmzn3yZNdd5pFzKVzldwUEiMcK3DzaXxDrc4bEfWoJyBhyhphj6RHj7ARqVZo9OW/rSlOoWMPvA91mx6ytu9TsOm5w/zV+7PX/koaesTMwX13oPst/vIXi9KENmSNNou4fa7Bsh8RCPEfRl0GP7lLvzxsM2kj0b2F+IODVC5h73kKdhL9rF3lJ8+Fn34m0cfHobCFlhHAfBhu77Ja0jiIMWOaRNv2vUpVAl7pj31k2eHLbyd5E4/Z+H7w4u9vs18M/HNl9p4k6xAZzI8Ol09nJi2BT/7dgTv5B78bwR3pVYnF1yx9kOSiCPCiMRYxlLC3aFJ0Jl9Q4XmJnfeNldwWDGkERCEcCUgMg4juDmqSQW3sFpfJlAN5ptXdj5NNbcYSZ3T2btIU5SErjM1615FB0Wa+QRFqdoywMPJ72D8IfjoSuFLIpAqk57FunJ3t56D6xgPGY1pSOKYQyc8XIX06vkHgsbHoobCdidinPmgYK2OFLXJYTdsnP2gFkX141OiRrvkn6tM3k+nla5dmODCwSc+VLf0nSu0eoYfylgMnzbE8IjiGEssqeAx5pw/X4X8x81eJfGItN0q1dlrP3GnT0nc6bOapi1Y/v+rRkDDfs7eB0iTwvch8uSa8nNIeCjRv/UwSPdgcO4nvDPDX5DlKZ57/k2lPSGsVjkjJIplRBrPFJzKSAoci0iELP5yx3xiqGxUO+DoX6iLl73ouG2Hp0fN868ZNal02mXhY8Mm5/F9YZOKMIw4CwUUATLm8tmi5ofPeMqlntnxQ0Hz/AFbqT/IYTtVzd6tDeyCIwqPoy8+fTtQIkIsWIhjLgiOpWhLRUJD3P8RzhQ2NApOaCSliCTYicb8iKi8E+rMfJGZxNSdijNbnHRBDKy5/ybxRuuFfYH7Pr8qVV7Z74c9zecrGqgll9Wul/Ytbt107xpU1WUBhethk2du6+4a1K55VqsfLjZ7zimYMyq/v6Y54ja87WLqES84rvS6Js1Ljh/+Whb1j61uEKz3I8H+a48algXbe3xNBzLVhbrSv2/jrPnWqdKlmXZfMrrvGXDQArx9NVmrsv5gwxbyXkgwZRGjYUhtpS7BUk0ViSklIY+pkMzmrX447Ct61H8v7b75af6J4fV/AVBLBwhp7RjmxAgAAGEhAABQSwECFAAUAAgACAC8jm5BRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIALyObkFp7RjmxAgAAGEhAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAXAkAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /><br /> | <ggb_applet width="603" height="627" version="4.0" ggbBase64="UEsDBBQACAAIALyObkEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAC8jm5BAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVabW/bthb+3P0KQhj24aK2+SZS6pwOSYDhFk3XosmG4X4ZaIl2uMiSJ8mOU+zH30NSkmU7cZM6d+0N4pAiD3l4znnOC+WMf1rPM7TSZWWK/CQgQxwgnSdFavLZSbCsp4Mo+On1d+OZLmZ6Uio0Lcq5qk8CbilNehJMNOaCRXSgYzEZ8KlMBxOC5YCohGOpxESSKEBoXZlXefGLmutqoRJ9mVzrubooElU7xtd1vXg1Gt3e3g5bVsOinI1ms8lwXaUBgmPm1UnQdF7BdluLbpkjpxiT0e/vLvz2A5NXtcoTHSArwtK8/u7F+NbkaXGLbk1aX58EgsQButZmdg0yyQhkGlmiBShkoZParHQFS3uPTuZ6vggcmcrt/AvfQ1knToBSszKpLk8CPJSUSS7jCAvCopixABWl0Xnd0JKG56jdbbwy+tZva3uOIw9QXRTZRNkd0d9/I4opRi9tQ3xDoRHCT2E/hplvqG+4b0JPw/1y7km5p+GehsMZV6Yyk0yfBFOVVaBBk09LsF73XNV3mXbnaQY20pOXIFNlPgExw6BSr3IYx/il/Qj4cNzouick6XGty+UTmbYsBWaPZ0mPEpS1PDmP9nnS8AExxQGmXu7HyEnCnmqBlft1nz2O7JCYuxz983EMBf9HRByPWlcZN96BqmtL26Cn1vPK+guLURhb2BMUgm8ICSgPEYmhkRSBNyASIh7CI4mQsK1ETMIERwxFyNIRhpxzhBH84dJtJlAIm9lRCT6JCDDiKGSIOJ/iCDwJOb8EH6UMKMIQhbDIsifUbsEE4gKeWIQ4nNG6pCRAyGAhPAN7ihhBzC4mElGBhN2PcOvqIrJHhy0pEhgJYjcErwaP9t4M9BFiVhrRqMvki2W9paJknrbdulh0tgBqiEebqOfj01ZQfDHO1ERnkCcurSURWqnMeoRjNC3yGjVGpNiPzUq1uDZJdanrGlZV6E+1Uheq1uufgbpqeTvapMirD2VRnxfZcp5XCCVFhrszFxnp9Wl3anhgvQnenwh7E6LXl/fyLWAGLSsN/IuyaslVmr6xFJvQAJp8n2d3Z6VWN4vCbIsxHrmUM9bLJDOpUflvAFbLxeoFdRnIhqs2A4Vx3B6kKNPLuwoQjNb/0WUBeozkUAiCRUQ4IxENA3TnZyDIDjkmEvKLIELEEk6WKOt6VMghpiGnhHKGJXC6e2AGtnOM9aqzj1rrTvRZad26Eds+vKnOimwz5IQ/V4t6WbrKATiVVqTTfJZpBxAXayEtJzeTYn3p3Zv5va7uFvDUwGQyc0pHEBhoCDLOmnbiW0djT9ZRYUeDHUUHNZN28ySmjsK1E986KsCuP1ojKWnFJLhlYyoXznCw5TQO+DbJL3NTX7QPtUluGkmJp/9lOZ/oDj7bW5Jn2nI82oHX+EaXuc4aNIMll8Wy8s7ZA3qqEzOHRz/RKERZY/0KB/CjqZ6Vuj135moyry43i/tA3Rt2W/1cFvM3+eoKkLBzgPGoPeW4SkqzsIBDE8gAN3qDqdRUChJI2l9n3Q9ET2yiAPXUVjXgmMv6ugBTz4ezIayDmAKj1vMyPYdCC9UOYA6jnarfuQrO6hQVkz8hrO2YYmMzmH4AbEhli2tla7xG7Ezd6XJLEW63d0Wqt+KjykH7Tgbw8IXdwNp3obVHhj8vdBawofOnrRgFGq/Q2rNFd037yVfvvny1klof22LqR/ctCF5rT+LGvn/3fYMqr7o9JebLuS5N0qnpo1MjrF02u3aH2FJtm+P9op40j1EueaRyyf3KvUe1+D7V9oVOivlc5SnKXcVybsok08EmhSpsAYQUsQrwcizrduKt36zZYk+DAOGe/t5+TRhuImANmfkGrh+VC9Odkmzn3yZNdd5pFzKVzldwUEiMcK3DzaXxDrc4bEfWoJyBhyhphj6RHj7ARqVZo9OW/rSlOoWMPvA91mx6ytu9TsOm5w/zV+7PX/koaesTMwX13oPst/vIXi9KENmSNNou4fa7Bsh8RCPEfRl0GP7lLvzxsM2kj0b2F+IODVC5h73kKdhL9rF3lJ8+Fn34m0cfHobCFlhHAfBhu77Ja0jiIMWOaRNv2vUpVAl7pj31k2eHLbyd5E4/Z+H7w4u9vs18M/HNl9p4k6xAZzI8Ol09nJi2BT/7dgTv5B78bwR3pVYnF1yx9kOSiCPCiMRYxlLC3aFJ0Jl9Q4XmJnfeNldwWDGkERCEcCUgMg4juDmqSQW3sFpfJlAN5ptXdj5NNbcYSZ3T2btIU5SErjM1615FB0Wa+QRFqdoywMPJ72D8IfjoSuFLIpAqk57FunJ3t56D6xgPGY1pSOKYQyc8XIX06vkHgsbHoobCdidinPmgYK2OFLXJYTdsnP2gFkX141OiRrvkn6tM3k+nla5dmODCwSc+VLf0nSu0eoYfylgMnzbE8IjiGEssqeAx5pw/X4X8x81eJfGItN0q1dlrP3GnT0nc6bOapi1Y/v+rRkDDfs7eB0iTwvch8uSa8nNIeCjRv/UwSPdgcO4nvDPDX5DlKZ57/k2lPSGsVjkjJIplRBrPFJzKSAoci0iELP5yx3xiqGxUO+DoX6iLl73ouG2Hp0fN868ZNal02mXhY8Mm5/F9YZOKMIw4CwUUATLm8tmi5ofPeMqlntnxQ0Hz/AFbqT/IYTtVzd6tDeyCIwqPoy8+fTtQIkIsWIhjLgiOpWhLRUJD3P8RzhQ2NApOaCSliCTYicb8iKi8E+rMfJGZxNSdijNbnHRBDKy5/ybxRuuFfYH7Pr8qVV7Z74c9zecrGqgll9Wul/Ytbt107xpU1WUBhethk2du6+4a1K55VqsfLjZ7zimYMyq/v6Y54ja87WLqES84rvS6Js1Ljh/+Whb1j61uEKz3I8H+a48algXbe3xNBzLVhbrSv2/jrPnWqdKlmXZfMrrvGXDQArx9NVmrsv5gwxbyXkgwZRGjYUhtpS7BUk0ViSklIY+pkMzmrX447Ct61H8v7b75af6J4fV/AVBLBwhp7RjmxAgAAGEhAABQSwECFAAUAAgACAC8jm5BRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIALyObkFp7RjmxAgAAGEhAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAXAkAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /><br /> | ||
(a) Was muss für <math>R</math> (Radius des großen, festen Kreises), <math>r</math> (Radius des abrollenden kleinen Kreises) und <math>d</math> (Abstand des beschreibenden Punktes zum Mittelpunkt <math>M_k</math> des abrollenden Kreises) gelten, damit eine Astroide entsteht?<br /><br /> | (a) Was muss für <math>R</math> (Radius des großen, festen Kreises), <math>r</math> (Radius des abrollenden kleinen Kreises) und <math>d</math> (Abstand des beschreibenden Punktes zum Mittelpunkt <math>M_k</math> des abrollenden Kreises) gelten, damit eine Astroide entsteht?<br /><br /> | ||
| − | |||
(b) Geben Sie eine Parameterdarstellung der Kurve an, auf der sich <math>M_k</math> der Mittelpunkt des abrollden Kreises bewegt. Verwenden Sie als Parameter den Winkel <math>\varphi</math>, dessen Schenkel die positive <math>x-</math>Achse und der Strahl <math>MM_k^+</math> sind.<br /><br /> | (b) Geben Sie eine Parameterdarstellung der Kurve an, auf der sich <math>M_k</math> der Mittelpunkt des abrollden Kreises bewegt. Verwenden Sie als Parameter den Winkel <math>\varphi</math>, dessen Schenkel die positive <math>x-</math>Achse und der Strahl <math>MM_k^+</math> sind.<br /><br /> | ||
(c) Wir stellen uns vor, dass mit dem abrollenden Kreis ein kartesisches Koordinatensystem <math>KS'</math>derart mitgeführt wird, dass die Achsen von <math>KS'</math> immer parallel zu den entsprechenden Achsen des globalen Koordinatensystems sind. Der Ursprung von <math>KS'</math> sei <math>M_k</math>:<br /><br /> | (c) Wir stellen uns vor, dass mit dem abrollenden Kreis ein kartesisches Koordinatensystem <math>KS'</math>derart mitgeführt wird, dass die Achsen von <math>KS'</math> immer parallel zu den entsprechenden Achsen des globalen Koordinatensystems sind. Der Ursprung von <math>KS'</math> sei <math>M_k</math>:<br /><br /> | ||
Version vom 28. November 2012, 11:53 Uhr
ParameterdarstellungenAufgabe 3.1Astroiden sind spezielle Hypozykloiden: (a) Was muss für Geben Sie eine Parameterdarstellung der Kurve an, die der Punkt Aufgabe 3.2Es seien Aufgabe 3.3Es sei gerichtete Größen, VektorenAufgabe 3.4Warum gelten gleichförmige Kreisbewegungen als beschleunigte Bewegungen? |
 (Radius des großen, festen Kreises),
(Radius des großen, festen Kreises),  (Radius des abrollenden kleinen Kreises) und
(Radius des abrollenden kleinen Kreises) und  (Abstand des beschreibenden Punktes zum Mittelpunkt
(Abstand des beschreibenden Punktes zum Mittelpunkt 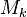 des abrollenden Kreises) gelten, damit eine Astroide entsteht?
des abrollenden Kreises) gelten, damit eine Astroide entsteht? , dessen Schenkel die positive
, dessen Schenkel die positive 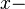 Achse und der Strahl
Achse und der Strahl 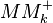 sind.
sind.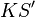 derart mitgeführt wird, dass die Achsen von
derart mitgeführt wird, dass die Achsen von  bezüglich
bezüglich 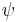 die der kleine Kreis auf dem großen Kreis abgerollt ist.
die der kleine Kreis auf dem großen Kreis abgerollt ist. an.
an.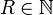 und
und 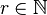 die Radien des großen, festen bzw. des kleinen abrollenden Kreises. Berechnen Sie, nach wieviel Umdrehungen des kleinen Kreises um seinen Mittelpunkt die entsprechende Hypozykloide geschlossen ist.
die Radien des großen, festen bzw. des kleinen abrollenden Kreises. Berechnen Sie, nach wieviel Umdrehungen des kleinen Kreises um seinen Mittelpunkt die entsprechende Hypozykloide geschlossen ist.
 gleichförmig auf einer Kreisbahn mit dem Radius
gleichförmig auf einer Kreisbahn mit dem Radius 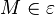 bewegt. Es gilt
bewegt. Es gilt 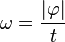 . Unter
. Unter 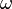 versteht man die Winkelgeschwindigkeit dieser Bewegung, wobei
versteht man die Winkelgeschwindigkeit dieser Bewegung, wobei 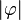 die Größe des überstrichenen Winkels und
die Größe des überstrichenen Winkels und  die dafür benötigte Zeit in Sekunden ist.
die dafür benötigte Zeit in Sekunden ist. 
