Lösung von Zusatzaufgabe 2.5P (WS 12 13): Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
Hier haben wir endlich eine korrekte Definiton des Kreises. Er liegt in einer Ebene und der Abstand zum Mittelpunkt ist immer der selbe.--[[Benutzer:Unicycle|Unicycle]] 16:01, 15. Nov. 2012 (CET) | Hier haben wir endlich eine korrekte Definiton des Kreises. Er liegt in einer Ebene und der Abstand zum Mittelpunkt ist immer der selbe.--[[Benutzer:Unicycle|Unicycle]] 16:01, 15. Nov. 2012 (CET) | ||
**Deine Begründung stimmt hier nicht, die Definition ist nicht korrekt. Wo liegt der Fehler?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:13, 16. Nov. 2012 (CET) | **Deine Begründung stimmt hier nicht, die Definition ist nicht korrekt. Wo liegt der Fehler?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:13, 16. Nov. 2012 (CET) | ||
| − | **Das <math>\left| MP \right|</math> ist falsch. Richtig wäre: Wenn für alle <math>X \in P</math> gilt: <math>\left| MX \right|</math> ist konstant, dann ist P ein Kreis mit Mittelpunkt M.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:23, 30. Nov. 2012 (CET) | + | **Das <math>\left| MP \right|</math> ist falsch. Richtig wäre: Wenn für alle <math>X \in P</math> gilt: <math>\left| MX \right|</math> ist konstant, dann ist P ein Kreis mit Mittelpunkt M.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:23, 30. Nov. 2012 (CET)<br /> |
| + | **Ja richtig! Allerdings muss man noch ausschließen, dass die Punktmenge nicht nur aus einem Punkt besteht, nämlich dem Mittelpunkt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:10, 30. Nov. 2012 (CET) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 30. November 2012, 12:10 Uhr
Welche Definition für Kreis ist richtig? Warum (nicht)?
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Wenn gilt:
eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
Die Definition ist nicht richtig, da sie nicht für eine Ebene definiert ist und somit z.B. eine Kugel oder Halbkugel nicht ausschließt.--Unicycle 15:47, 15. Nov. 2012 (CET)
- Sei
 ein Punkt und
ein Punkt und  eine Punktmenge. Wenn gilt:
eine Punktmenge. Wenn gilt: 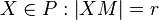 , dann ist
, dann ist  ein Kreis.
ein Kreis.
Das gleiche wie oben, man kann damit auch eine Kugel konstruieren.--Unicycle 16:01, 15. Nov. 2012 (CET)
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  alle Punkte
alle Punkte 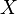 enthält für die gilt∶
enthält für die gilt∶  und
und 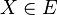 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
Auch hier ist es noch nicht sauber definiert, da nicht ausgeschlossen ist, dass P noch mehr Punkte außer X enthält. Man müsste hier schreiben "...Wenn P nur die Punkte X enthält..."--Unicycle 16:01, 15. Nov. 2012 (CET)
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  genau alle Punkte
genau alle Punkte 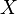 enthält für die gilt∶
enthält für die gilt∶  und
und 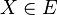 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
Hier ist zwar das Problem von oben erkannt, aber nicht richtig umgesetzt. Das genau alle betont lediglich, dass auch wirklich alle X in P enthalten sind, schließt aber immernoch nicht aus, dass P mehr Punkte als nur die Punkte X enthält.--Unicycle 16:01, 15. Nov. 2012 (CET)
- "Genau alle Punkte X" bedeutet, dass alle und nur diese Punkte X enthalten sind. Damit wäre das Problem aus Definition 3 gelöst. Ich bin mir jetzt allerdings auch nicht 100% sicher.--Tutorin Anne 14:13, 16. Nov. 2012 (CET)
- "Genau alle Punkte X" bedeutet, dass alle und nur diese Punkte X enthalten sind. Damit wäre das Problem aus Definition 3 gelöst. Ich bin mir jetzt allerdings auch nicht 100% sicher.--Tutorin Anne 14:13, 16. Nov. 2012 (CET)
Tutorin Anne hat recht!--Schnirch 14:47, 16. Nov. 2012 (CET)
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Menge, deren Elemente Punkte sind. Wenn für alle
eine Menge, deren Elemente Punkte sind. Wenn für alle 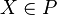 gilt∶
gilt∶  , dann ist
, dann ist  ein Kreis.
ein Kreis.
Auch hier ist es wieder das gleiche Problem. Man müsste schreiben "...,dann beschreibt die Menge aller X \in P einen Kreis." --Unicycle 16:01, 15. Nov. 2012 (CET)
- Die Begründung stimmt so nicht. "Für alle X Element P gilt" heißt, dass eben für jedes der Elemente aus P diese Bedingung gelten muss. Das Problem liegt wo anders.--Tutorin Anne 14:13, 16. Nov. 2012 (CET)
- Die Begründung stimmt so nicht. "Für alle X Element P gilt" heißt, dass eben für jedes der Elemente aus P diese Bedingung gelten muss. Das Problem liegt wo anders.--Tutorin Anne 14:13, 16. Nov. 2012 (CET)
Dann müsste es doch heißen "dann ist X ein Kreis", oder?--Der Bohrer 11:03, 22. Nov. 2012 (CET)
X ist ein beliebiger Punkt, keine Menge und damit auch kein Kreis. --Tutorin Anne 15:27, 22. Nov. 2012 (CET)
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Alle Elemente von
eine Menge, deren Elemente Punkte sind. Alle Elemente von  liegen in ein und derselben Ebene wie
liegen in ein und derselben Ebene wie  . Wenn gilt:
. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
Hier haben wir endlich eine korrekte Definiton des Kreises. Er liegt in einer Ebene und der Abstand zum Mittelpunkt ist immer der selbe.--Unicycle 16:01, 15. Nov. 2012 (CET)
- Deine Begründung stimmt hier nicht, die Definition ist nicht korrekt. Wo liegt der Fehler?--Tutorin Anne 14:13, 16. Nov. 2012 (CET)
- Das
 ist falsch. Richtig wäre: Wenn für alle
ist falsch. Richtig wäre: Wenn für alle 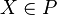 gilt:
gilt: 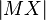 ist konstant, dann ist P ein Kreis mit Mittelpunkt M.--Der Bohrer 11:23, 30. Nov. 2012 (CET)
ist konstant, dann ist P ein Kreis mit Mittelpunkt M.--Der Bohrer 11:23, 30. Nov. 2012 (CET)
- Ja richtig! Allerdings muss man noch ausschließen, dass die Punktmenge nicht nur aus einem Punkt besteht, nämlich dem Mittelpunkt.--Tutorin Anne 12:10, 30. Nov. 2012 (CET)

