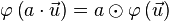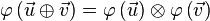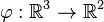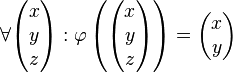Lineare Abbildungen, Vektorraumisomorphismus 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎senkrechte Parallelprojektion)
(→‎senkrechte Parallelprojektion auf die x-y-Ebene)
Zeile 12: Zeile 12:
 
Man beweise: <math>\varphi</math> ist lineare Abbildung
 
Man beweise: <math>\varphi</math> ist lineare Abbildung
  
−
 
+
=Isomorphe Vektorräume=
 +
{{Definition|Zwei Vektorräume sind isomorph zu einender, wenn sie durch eine bijektive  lineare Abbildung aufeinander abgebildet werden können. }}
  
 
<!--- hier drunter nichts eintragen --->
 
<!--- hier drunter nichts eintragen --->

Version vom 12. Dezember 2012, 19:16 Uhr

Inhaltsverzeichnis

Definition

Definition

(lineare Abbildung)
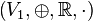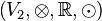Es seien \left(V_1, \oplus, \mathbb{R}, \cdot\right) und \left(V_2, \otimes, \mathbb{R}, \odot\right) zwei Vektorräume über der Körper der reellen Zahlen.
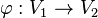Eine Abbildung \varphi: V_1 \rightarrow V_2 heißt lineare Abbildung wenn gilt: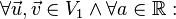
\forall \vec{u}, \vec{v} \in V_1 \wedge \forall a \in \mathbb{R}:
(H) \varphi ist homogen: \varphi\left(a \cdot \vec{u} \right) = a \odot \varphi\left(\vec{u}\right)
(A) \varphi ist additiv: \varphi\left(\vec{u} \oplus \vec{v} \right)= \varphi \left(\vec{u}\right) \otimes \varphi \left(\vec{v}\right)

Beispiele

senkrechte Parallelprojektion auf die x-y-Ebene

\varphi: \mathbb{R}^3 \rightarrow \mathbb{R}^2
\forall \begin{pmatrix} x \\ y \\ z \end{pmatrix}: \varphi \left( \begin{pmatrix} x \\ y \\ z \end{pmatrix}\right)= \begin{pmatrix} x \\ y \end{pmatrix}
Man beweise: \varphi ist lineare Abbildung

Isomorphe Vektorräume

Definition

Zwei Vektorräume sind isomorph zu einender, wenn sie durch eine bijektive lineare Abbildung aufeinander abgebildet werden können.

Von „http://geometrie.zum.de/index.php?title=Lineare_Abbildungen,_Vektorraumisomorphismus_2012_13&oldid=19636“