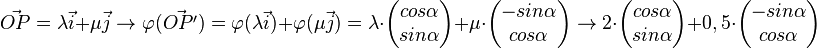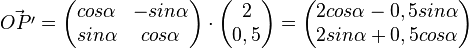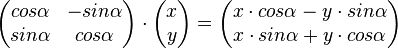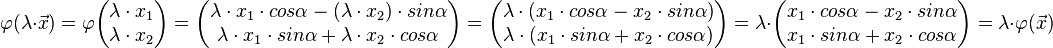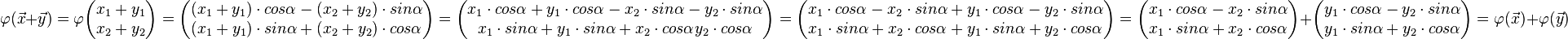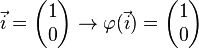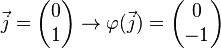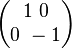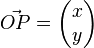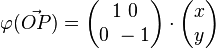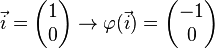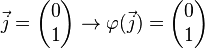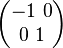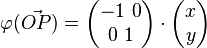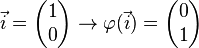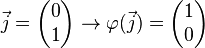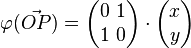Definition
Beispiele
senkrechte Parallelprojektion auf die x-y-Ebene
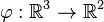
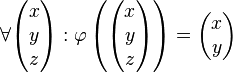
Man beweise:  ist lineare Abbildung ist lineare Abbildung
Drehung
Drehungen um den Ursprung des Koordinatensystems
Drehung der kanonischen Basisvektoren
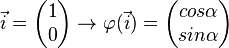
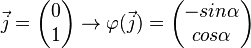
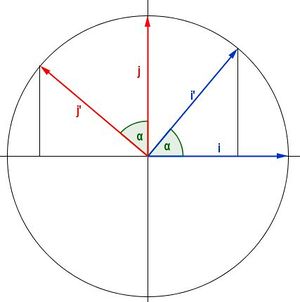
Drehung anderer Vektoren:
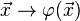
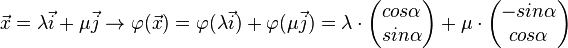
Bsp.: 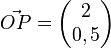 wird an O um wird an O um  gedreht. gedreht.
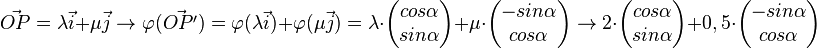
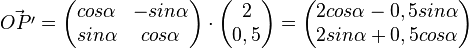
Drehungsmatrix:
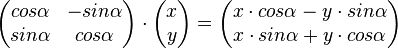
Drehung um den Ursprung des Koordinatensystems als lineare Abbildung:
Behauptung:  ist eine lineare Abbildung. ist eine lineare Abbildung.
Zu zeigen:
(H)  ist homogen ist homogen
(A)  ist additiv ist additiv
Beweis zur Homogenität:
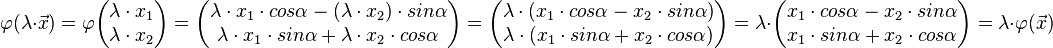
Beweis zur Additivität:
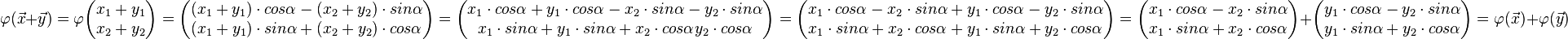
Geradenspiegelung
Spiegelung an der x-Achse:
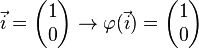
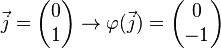
Matrix für die Spiegelung an der x-Achse:
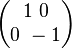
Spiegelung eine Punktes P an der x-Achse:
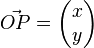
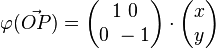
Spiegelung an der x-Achse als lineare Abbildung:
Behauptung:  ist eine lineare Abbildung. ist eine lineare Abbildung.
Zu zeigen:
(H)  ist homogen ist homogen
(A)  ist additiv ist additiv
Beweis zur Homogenität:
Beweis zur Addidtivität:
--Jessy* 09:15, 16. Jan. 2013 (CET)
Spiegelung an der y-Achse:
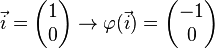
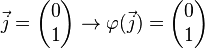
Matrix für die Spiegelung an der y-Achse:
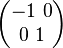
Spiegelung eine Punktes P an der y-Achse:
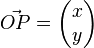
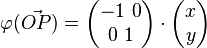
Spiegelung an der y-Achse als lineare Abbildung:
Behauptung:  ist eine lineare Abbildung. ist eine lineare Abbildung.
Zu zeigen:
(H)  ist homogen ist homogen
(A)  ist additiv ist additiv
Beweis zur Homogenität:
Beweis zur Addidtivität:
--Jessy* 09:15, 16. Jan. 2013 (CET)
Spiegelung an der 1. Winkelhalbierenden:
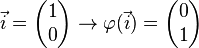
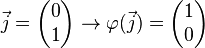
Matrix für die Spiegelung an der 1. Winkelhalbbierenden:

Spiegelung eine Punktes P an der 1. Winkelhalbbierenden:
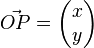
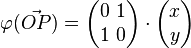
Spiegelung an der 1. Winkelhalbierenden als lineare Abbildung:
Behauptung:  ist eine lineare Abbildung. ist eine lineare Abbildung.
Zu zeigen:
(H)  ist homogen ist homogen
(A)  ist additiv ist additiv
Beweis zur Homogenität:
Beweis zur Addidtivität:
--Jessy* 09:16, 16. Jan. 2013 (CET)
Zentrische Streckung
Isomorphe Vektorräume
Definition
Zwei Vektorräume sind isomorph zu einander, wenn sie durch eine bijektive lineare Abbildung aufeinander abgebildet werden können.
| 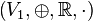 und
und 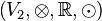 zwei Vektorräume über der Körper der reellen Zahlen.
zwei Vektorräume über der Körper der reellen Zahlen. 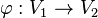 heißt lineare Abbildung wenn gilt:
heißt lineare Abbildung wenn gilt: 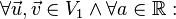
 ist homogen:
ist homogen: 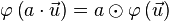
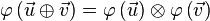
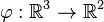
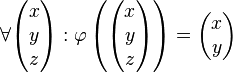
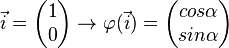
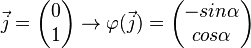

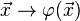
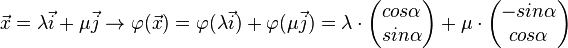
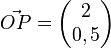 wird an O um
wird an O um  gedreht.
gedreht.