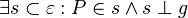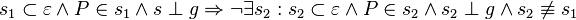Lösung Aufgabe 9.7 WS 12 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
Hauler (Diskussion | Beiträge) (→Lösung von User ...) |
||
| Zeile 11: | Zeile 11: | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
| + | Lautet die Voraussetzung: Existenz ebene und g Element der ebene und p Element g | ||
| + | Lautet die Behauptung : P Element s und s orthogonal zu g | ||
| + | |||
| + | --[[Benutzer:Hauler|Hauleri]] 14:36, 25. Jan. 2013 (CET) | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
Version vom 25. Januar 2013, 14:36 Uhr
Aufgabe 9.7In der Ebene Lösung von User ...Lautet die Voraussetzung: Existenz ebene und g Element der ebene und p Element g Lautet die Behauptung : P Element s und s orthogonal zu g --Hauleri 14:36, 25. Jan. 2013 (CET) Lösung von User ... |
 seien eine Gerade
seien eine Gerade  und ein Punkt
und ein Punkt  mit
mit 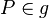 gegeben.
gegeben.