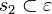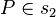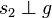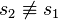Aufgabe 9.7
In der Ebene  seien eine Gerade seien eine Gerade  und ein Punkt und ein Punkt  mit mit 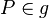 gegeben. gegeben.
Beweisen Sie:
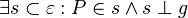
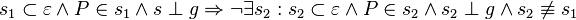
Tippfehler:
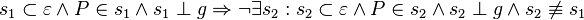
Lösung von User ...
Lautet die Voraussetzung: Existenz ebene und g Element der ebene und p Element g
Lautet die Behauptung : P Element s und s orthogonal zu g
--Hauleri 14:36, 25. Jan. 2013 (CET)
Bemerkung --*m.g.* 13:25, 26. Jan. 2013 (CET)
Das steht so nirgends:
Voraussetzung:
In der Ebene  seien eine Gerade seien eine Gerade  und ein Punkt und ein Punkt  mit mit 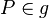 gegeben. gegeben.
Wir gehen also von einer Ebene  aus. Ob die Existiert schert uns wenig. In aus. Ob die Existiert schert uns wenig. In  möge eine Gerade möge eine Gerade  gelegen sein und auf dieser Geraden ein Punkt gelegen sein und auf dieser Geraden ein Punkt  . Sollte eine derartige Konstellation vorliegen, wissen wir Folgendes: . Sollte eine derartige Konstellation vorliegen, wissen wir Folgendes:
Behauptung 1
Wir übersetzen:
| Mathe |
Deutsch
|
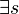 |
Es existiert eine Gerade  , ,
|
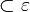 |
die zu der Ebene  gehört gehört
|
| : |
und die folgenden Eigenschaften hat:,
|
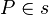 |
der Punkt  gehört zu gehört zu  bzw. anders ausgedrückt bzw. anders ausgedrückt  geht durch geht durch 
|
 |
und
|
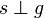 |
 steht senkrecht auf steht senkrecht auf 
|
Noch mal neu:
- Zu jeder Geraden
 und jedem Punkt und jedem Punkt  auf dieser Geraden auf dieser Geraden  gibt es in jeder Ebene, die gibt es in jeder Ebene, die  enthält eine zu enthält eine zu  senkrechte Gerade senkrechte Gerade  , die durch , die durch  geht. geht.
Oder:
- In jeder Ebene, die eine Gerade enthält, gibt es in jedem Punkt dieser Geraden eine Senkrechte zu der Geraden.
Behauptung 2
Wir sehen den Implikationspfeil und setzen vor alles, was vor dem Pfeil steht ein Wenn:
Wenn
| Mathe |
Deutsch
|
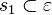 |
die Gerade 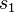 zur Ebene zur Ebene  gehört gehört
|
 |
und
|
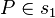 |
durch den Punkt  geht geht
|
 |
und
|
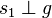 |
senkrecht auf  steht steht
|
Jetzt kommt der Implikationspfeil 
Wir übersetzen ihn mit
Dann:
| Mathe |
Deutsch
|
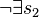 |
existiert keine Gerade 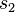 , ,
|
 |
die die folgenden Eigenschaften hat:
|
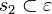 |
sie gehört (auch) zur Ebene 
|
 |
und
|
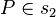 |
geht (auch) durch den Punkt 
|
 |
und
|
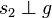 |
steht (auch) senkrecht auf 
|
 |
und
|
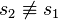 |
sie ist von der Geraden 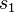 verschieden. verschieden.
|
Kurzübersetzung:
Es kann nur eine geben.
Hinweis: Sie sollten für die Klausur in der Lage sein, sowas in angemessener Zeit korrekt zu übersetzen.
--*m.g.* 14:23, 26. Jan. 2013 (CET)
Bezug zur Schule:
Das Ganze entspricht in gewisser Weise dem Erkennen und Übersetzen der Struktur von Termen in den Klassen 8 aufwärts.
Lösung von User ...
|
 seien eine Gerade
seien eine Gerade  und ein Punkt
und ein Punkt  mit
mit 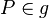 gegeben.
gegeben.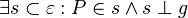
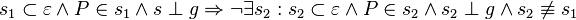
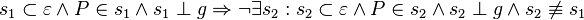
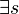
 ,
,
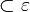
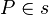

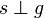
 und jedem Punkt
und jedem Punkt 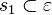
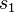 zur Ebene
zur Ebene 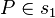
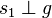

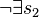
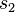 ,
,