Lösung von Zusatzaufgabe 6.1P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 24: | Zeile 24: | ||
Ich bin mir aber nicht sicher, ob man das so machen kann, kommt mir irgendwie zu primitiv vor...--[[Benutzer:Unicycle|Unicycle]] 22:13, 17. Jan. 2013 (CET)<br /> | Ich bin mir aber nicht sicher, ob man das so machen kann, kommt mir irgendwie zu primitiv vor...--[[Benutzer:Unicycle|Unicycle]] 22:13, 17. Jan. 2013 (CET)<br /> | ||
*Du hast nicht begründet, wie du auf den zweiten Schritt kommst. Wo steht denn das? | *Du hast nicht begründet, wie du auf den zweiten Schritt kommst. Wo steht denn das? | ||
| − | * Tipp: Schaut euch mal an, was unter Dreiecksungleichung steht.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:44, 18. Jan. 2013 (CET) | + | * Tipp: Schaut euch mal an, was unter Dreiecksungleichung steht.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:44, 18. Jan. 2013 (CET)<br /><br /> |
| − | + | Hier fehlt noch etwas vor Schritt 2)<br /><br /> | |
| + | Man muss hier eine Fallunterscheidung machen:<br /> | ||
| + | Fall1: <math>|AB| + |BC| > |AC|\Rightarrow</math> <math>\exists</math> Dreieck ABC -> ist zu verwerfen,da Widerspruch zu 1.)<br /> | ||
| + | Fall2: <math>|AB| + |BC| = |AC|\Rightarrow</math> <math>\neg \exists</math> Dreieck ABC -> ist anzunehmen, daraus folgt dann Punkt 2<br /> | ||
| + | Begründung: Dreiecksungleichung, 1.)<br /> | ||
| + | --[[Benutzer:TobiWan|TobiWan]] 14:15, 19. Jan. 2013 (CET)<br /> | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 19. Januar 2013, 14:15 Uhr
Beweisen Sie: Aus 
folgt 
.
Zum Verwenden von mathematischen Zeichen, kann man den Formeleditor öffnen (Symbol ganz links, Summenzeichen). Als Hilfestellung schon mal eine Tabelle. --Tutorin Anne 12:38, 10. Dez. 2012 (CET)
| Voraussetzung | Zw (A,B,C) |
| Behauptung | koll (A,B,C) |
| Beweisschritt | Begründung |
|---|---|
1  |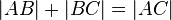
Voraussetzung, Def. Zwischenrelation |
2  |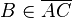
1.) |
3  |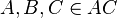
1,) ; 2,) |
| 4 koll (A,B,C) | 3.); Def. koll |
Ich bin mir aber nicht sicher, ob man das so machen kann, kommt mir irgendwie zu primitiv vor...--Unicycle 22:13, 17. Jan. 2013 (CET)
- Du hast nicht begründet, wie du auf den zweiten Schritt kommst. Wo steht denn das?
- Tipp: Schaut euch mal an, was unter Dreiecksungleichung steht.--Tutorin Anne 18:44, 18. Jan. 2013 (CET)
Hier fehlt noch etwas vor Schritt 2)
Man muss hier eine Fallunterscheidung machen:
Fall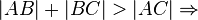1: 
Dreieck ABC -> ist zu verwerfen,da Widerspruch zu 1.)
Fall2: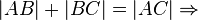 
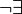Dreieck ABC -> ist anzunehmen, daraus folgt dann Punkt 2
Begründung: Dreiecksungleichung, 1.)
--TobiWan 14:15, 19. Jan. 2013 (CET)
