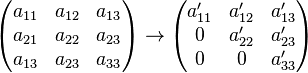Gauß-Algorithmus: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „==Gauß-Algorithmus== Der Gauß-Algorithmus (oder Gauß-Eliminationsverfahren oder "Gauß") ist ein Algorithmus zur Lösung von Linearen Gleichungssystemen (LGS)…“) |
(→Gauß-Algorithmus) |
||
| Zeile 11: | Zeile 11: | ||
<math>\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33} \end{pmatrix} \rightarrow \begin{pmatrix} a'_{11} & a'_{12} & a_{13}'\\ 0 & a'_{22} & a'_{23}\\0 & 0 & a'_{33} \end{pmatrix} </math> | <math>\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33} \end{pmatrix} \rightarrow \begin{pmatrix} a'_{11} & a'_{12} & a_{13}'\\ 0 & a'_{22} & a'_{23}\\0 & 0 & a'_{33} \end{pmatrix} </math> | ||
| + | |||
| + | |||
| + | [[Kategorie:Linalg]] | ||
Version vom 30. April 2013, 11:03 Uhr
Gauß-Algorithmus
Der Gauß-Algorithmus (oder Gauß-Eliminationsverfahren oder "Gauß") ist ein Algorithmus zur Lösung von Linearen Gleichungssystemen (LGS).
Das Grundprinzip besteht darin, die Matrix auf Stufen- bzw. Dreiecksform zu bringen, um so die Lösungsmenge leicher 'ablesen' zu können.
Im Gauß-Verfahren werden folgende Schritt (Äquivalenzumformungen) verwendet, die die Lösung des LGS nicht verändern.
- Vertauschen von zwei Gleichungen
- Multiplikaiton einer Gleichung mit einer reelen Zahl (
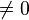 )
)
- Addition von zwei Gleichung