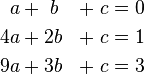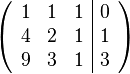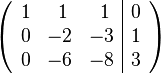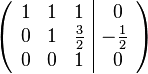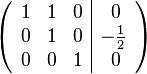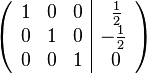Gauß-Algorithmus

Gauß-Algorithmus

Der Gauß-Algorithmus (oder Gauß-Eliminationsverfahren) ist ein Algorithmus zur Lösung von Linearen Gleichungssystemen (LGS). Das Grundprinzip besteht darin, die Matrix auf Stufen- bzw. Dreiecksform zu bringen, um so die Lösungsmenge leicher 'ablesen' zu können. Im Gauß-Verfahren werden folgende Schritt (Äquivalenzumformungen) verwendet, die die Lösung des LGS nicht verändern.

• Vertauschen von zwei Gleichungen
• Multiplikaiton einer Gleichung mit einer reelen Zahl ($\neq 0$)
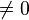• Addition von zwei Gleichung

Die Äquivalenzumformugen ändern die Lösungsmenge des gegebenen LGS nicht.

$\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33} \end{pmatrix} \rightarrow \begin{pmatrix} a'_{11} & a'_{12} & a_{13}'\\ 0 & a'_{22} & a'_{23}\\0 & 0 & a'_{33} \end{pmatrix}$

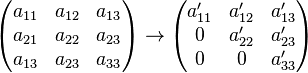
Gauß Jordan Algorithmus

Der Gauß-Jordan- Algorithmus ist der erweiterte Gauß-Algorithmus, der es ermöglicht die Lösungen direkt abzulesen, statt dem "Einsetzen von unten nach oben" die Lösungen zu berechnen. Der Gauß Jordan Algorithmus bringt die Matrix in Diagonalform, statt nur auf Stufenform.

$\begin{pmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33} \end{pmatrix} \rightarrow \begin{pmatrix} a'_{11} & 0 & 0\\ 0 & a'_{22} &0\\0 & 0 & a'_{33} \end{pmatrix}$

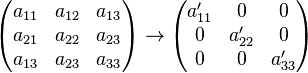
Beispiel

Es ist das folgende lineare Gleichungssystem gegeben:

$\begin{align} a &+ \ b&+ \ c = 0\\ 4a &+ 2b&+ \ c = 1\\ 9a &+ 3b&+ \ c = 3 \end{align}$

Es wird nun die erweiterte Koeffizientenmatrix des Gleichungssystems gebildet. In der ersten Spalte stehen die Faktoren der Variable a, in der zweiten die der Variable b, in der dritten die der Variable c und in der vierten die rechte Seite des Gleichungssystems. Ziel ist es nun, dass auf der linken Seite die Einheitsmatrix steht:

$\left(\begin{array}{ccc|c} 1 & 1 & 1 & 0 \\ 4 & 2 & 1 & 1 \\ 9 & 3 & 1 & 3 \end{array}\right)$

Es werden nun folgende Zeilentransformationen vorgenommen:

• Zu Zeile 2 wird addiert: -4 * Zeile 1.
• Zu Zeile 3 wird addiert: -9 * Zeile 1.

Damit ergibt sich:

$\left(\begin{array}{ccc|c} 1 &\ 1 &\ 1 & 0 \\ 0 & -2 & -3 & 1 \\ 0 & -6 & -8 & 3 \end{array}\right)$

• Zu Zeile 3 wird addiert: -3 * Zeile 2.
• Zeile 2 wird dividiert durch -2.

$\left(\begin{array}{ccc|c} 1 & 1 & 1 &\ 0 \\ 0 & 1 & {3 \over 2} & -{1 \over 2} \\ 0 & 0 & 1 &\ 0 \end{array}\right)$

Hier endet der Gauß-Algorithmus, aber der Gauß-Jordan Algorithmus bringt die Matrix auf Diagonalform

• Zu Zeile 1 wird addiert: -1 * Zeile 3.
• Zu Zeile 2 wird addiert: -3/2 * Zeile 3.

$\left(\begin{array}{ccc|c} 1 & 1 & 0 &\ 0 \\ 0 & 1 & 0 &-{1 \over 2} \\ 0 & 0 & 1 &\ 0 \end{array}\right)$

• Zu Zeile 1 wird addiert: -1 * Zeile 2.

$\left(\begin{array}{ccc|c} 1 & 0 & 0 &\ {1 \over 2} \\ 0 & 1 & 0 & -{1 \over 2} \\ 0 & 0 & 1 &\ 0 \end{array}\right)$

Diese Matrix wird auf unsere Gleichungen zurück übertragen. Wir erhalten:

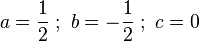$a = \frac{1}{2} \; ; \ b = -\frac{1}{2} \; ; \ c = 0$ .

Einzelnachweise

[1]