Serie 11 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 11.04) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 10.05) |
||
| Zeile 22: | Zeile 22: | ||
==Aufgabe 10.05 == | ==Aufgabe 10.05 == | ||
| − | + | Beweisen Sie: Jedes Dreieck hat genau einen Umkreis.<br /> | |
[[Lösung von Aufg. 11.05_SoSe_13]] | [[Lösung von Aufg. 11.05_SoSe_13]] | ||
Version vom 7. Juli 2013, 16:31 Uhr
Aufgabe 11.01Im Folgenden beziehen wir uns auf die Beweisführung zum schwachen Außenwinkelsatz in der Vorlesung vom letzten Freitag (5. Juli). Beweisen Sie, dass der Punkt Aufgabe 11.02Es sei bereits bewiesen, dass der größeren Seite eines Dreiecks auch der größere Winkel gegenüber liegt. Beweisen Sie die Umkehrung dieses Satzes. Lösung von Aufg. 11.02_SoSe_13 Aufgabe 11.03Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt auf eine Gerade. Aufgabe 11.04Definieren Sie den Begriff Umkreis eines Dreiecks. Lösung von Aufg. 11.04_SoSe_13 Aufgabe 10.05Beweisen Sie: Jedes Dreieck hat genau einen Umkreis. Aufgabe 11.06Lösung von Aufg. 11.06_SoSe_13 Aufgabe 11.07Lösung von Aufg. 11.07_SoSe_13 Aufgabe 11.08Lösung von Aufgabe 11.08_SoSe_13 Aufgabe 11.09Lösung von Aufgabe 11.09_SoSe_13 Aufgabe 11.10 |
in der offenen Halbebene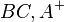 
liegt.
