Übung 2: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Parabel: y(x)=ax^2) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 6) |
||
| Zeile 22: | Zeile 22: | ||
===Aufgabe 6=== | ===Aufgabe 6=== | ||
| − | Gegeben sei die Parabel <math>p</math> durch <math>y(x)=ax^2, a \in \mathbb{R} a \not= 0</math>. Man beweise | + | Gegeben sei die Parabel <math>p</math> durch <math>y(x)=ax^2, a \in \mathbb{R}, a \not= 0</math>. Man beweise: ein zur y-Achse paralleler Lichtstrahl <math>w</math>, der von innen auf <math>p</math> trifft, wird so reflektiert, dass er durch den Brennpunkt <math>F</math> von <math>p</math> geht. |
Version vom 16. November 2013, 19:00 Uhr
Inhaltsverzeichnis |
Faltkonstruktion der Parabel
Normalparabel
Es sei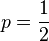 
, 
.
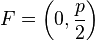Die Gerade 
sei durch die Gleichung 
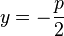gegeben. 
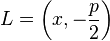sei ein beliebiger Punkt auf .
Der Punkt 
sei der Schnittpunkt der Mittelsenkrechten 
von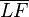 
mit der in 
auf errichteten Senkrechten 
.
Aufgabe 1
Man beweise: ist Tangente an die Normalparabel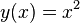 
in .
Aufgabe 2
Man beweise: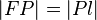 
.
Aufgabe 3
Gegeben sei der Punkt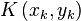 
. Man beweise:
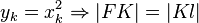
Parabel: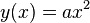 
Aufgabe 4
Die Lösung der Aufgaben 2 und 3 hätte sich nicht zwangsläufig auf die Normalparabel beziehen müssen. Formulieren Sie eine Definition für den Begriff Parabel:
Definition
Parabel
Es seien eine Gerade und 
ein Punkt außerhalb von . Unter der Parabel mit der Leitgeraden und dem Brennpunkt versteht man die Menge aller Punkte mit ... .
Aufgabe 5
Der Brennpunkt einer Parabel mit der Funktionsgleichung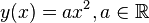 
habe zur Leitgeraden den Abstand 
. Man drücke 
mittels aus.
Aufgabe 6
Gegeben sei die Parabel durch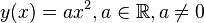 
. Man beweise: ein zur y-Achse paralleler Lichtstrahl 
, der von innen auf trifft, wird so reflektiert, dass er durch den Brennpunkt von geht.
