Übung 2: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 6) |
*m.g.* (Diskussion | Beiträge) (→Faltkonstruktion der Parabel) |
||
| Zeile 23: | Zeile 23: | ||
===Aufgabe 6=== | ===Aufgabe 6=== | ||
Gegeben sei die Parabel <math>p</math> durch <math>y(x)=ax^2, a \in \mathbb{R}, a \not= 0</math>. Man beweise: ein zur y-Achse paralleler Lichtstrahl <math>w</math>, der von innen auf <math>p</math> trifft, wird so reflektiert, dass er durch den Brennpunkt <math>F</math> von <math>p</math> geht. | Gegeben sei die Parabel <math>p</math> durch <math>y(x)=ax^2, a \in \mathbb{R}, a \not= 0</math>. Man beweise: ein zur y-Achse paralleler Lichtstrahl <math>w</math>, der von innen auf <math>p</math> trifft, wird so reflektiert, dass er durch den Brennpunkt <math>F</math> von <math>p</math> geht. | ||
| + | =Experimentierumgebungen:= | ||
| + | ==Normalparabel== | ||
| + | <ggb_applet width="850" height="554" version="4.2" ggbBase64="UEsDBBQACAgIAHWYcEMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAB1mHBDAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1ZW2/buBJ+7v6KgbAPLRDbpG6WCruLpEBwCqQXnHQXB+dhF5RE29zIko4kO3bRH3+GpCjLVnNxnN1NU4ekNBzOfDPzkXQmv2yWKax5WYk8m1p0SCzgWZwnIptPrVU9GwTWL+9+msx5PudRyWCWl0tWTy13aFu7eTga+kROFsnUmvHYZm4YDWaRSweu53oDFgbuwPHcWeyElMaOawFsKvE2yz+xJa8KFvPreMGX7CqPWa10Luq6eDsa3d7eDs3qw7ycj+bzaLipEgvQ8qyaWk3nLarbm3TrKHGbEDr6z8crrX4gsqpmWcwtkF6txLufXk1uRZbkt3ArknoxtYLx2IIFF/MFuumH1IKRFCrQ14LHtVjzCqd2hsrnellYSoxl8v0r3YO0dceCRKxFwsupRYbUs8eh41PXCz2bktC3IC8Fz+pG2Cw6Muoma8FvtV7ZU0u6JERL16ISUcoRdZZW6JbIZiVCihaVKxxW9TblESvNeGcQPcMfFBDfuNSFsdM4TC07JGc2HZ+NCTnzPKJt6S5sQZ3nqdJKwAvh+3ewiU3gTDZUNzY2vq9fEf2MOLqxdePqxtMyrp7ualFXy7haxnXu8bMZ7xxtHux5avx0un5S9E9+fPwoAA78DDp+UunEd6DSetU4IO2myn7ZuM3Q18OxaijRDW1eBvKXwss/0SPnSR7Rzqo6H+5etJcvZsXAO2JF+yQ/Wy+pZIzDNW3vDi9PBLddtOsorqX+q09vSecoP++E9ogVffeU2n/CgmOyV/am5nVLm/Y+GJ7NqMnIsOGkMQiqhZRtUrrmy0qa6ISKnICCh8Xrj5FLPKAhNmNZxDZQD1wPhzQAX7ZjcGTduuBAAFKOOqAoyAvwl6tq2gcPdcmHY13c4LjgOUAVcbmAKIAiP8TEdlDC88DDSXJ1Kpd1fHB9HDgBuGigpL2xpBYH5+EYF7fBoeDIuXQMtg++DWNJndSVjOoH0nZUaoNPwJdTkTuRNzVn4owAHOkNVkGRV6IFd8HToo2KwlFkxarewy5eJqZb5wfSSR7fXBxgzVlVmz4K4Ya12xf1Bra3bb6apCziKR4urmUaAKxZKqtc6Z/lWQ0mBWz9bF6yYiHi6prXNc6q4E+2Zles5ptLlK6MgWpptZtP+CpORSJY9hvmiFQhFUK7ucvUMpu7Z/t6lTjPy+R6W2HiwOa/vMzRptAf+k7g0zAMHIq7IW612+ZVgCcdH3kXldmEepi2MZMJ73p06Dhj4vg+oYEdhlii2zveNf7xdesZ2/DKQDkvRdLtf6gu8jRpw1HkIqvfs6JeleqchjRZSpfOs3nKFbKKePHEE99E+ea6oVCt6+u2wBHR60fz93mal4DlaHvoybxpI90qGWlYK0WUDFESxMRIJO17ip5JCdVGulVSGHRtWuMoNV5SYpYRlSIaVN5NMZUx8vy0ykR9ZQa1iG8aT6mW/7RaRphszbR9lfSZVE5GB+k1ueFlxlOdRBkGcpWvKp3VbWa+mqwq/oXVi/Ms+TefYzl+YZIRa1StRXcWJzwWS5yonzfQMRnWX9FU/TTh85IbD1N1MNbAqrekm9K9x0rVZZkvP2Trr5gzB6ZORsafSRWXopCZCRFS9A3fZV8iKoYEn3TnofMVehFLskEgawmiBWxVL/JSnX2xZOXGDJ/yNZegIk1iQsp6TfkSD75Qq7TMVkteirgNkT5Uo5Er48ewyUoZH8ijP5Fbdnu4nrSDE9/fkbnA0mLB1Fm8yU+2Rau6WCltH/OkWZkaBDFAyk2ki0KnSsG5TrK6qS0oUJ0qzQ60jafS501R8kpenYzJDKl0g9q2MIXXg+INjMA26mTlaHbdx0o/bxX0QNnL9eMwIfdi8nk2q3gNG2S1EBlOUcuPEHM6qVhJcXVD3DbXzG9ybHuH7FAj3d/gpadSFNYCKjv/EknCszYS/H+ZnlLpokUAUxGLulkV6VECrCz5Of354RhcNjF4Tc6gkAF4Y9ZXfPujEDQvWgVPiYEfqCDIJtLNI8PwCKAVwBJpanQpi+WGsDdTP+2TyB6Gl30M98BADuhUbvKPJOTAVX479+J0WMKSAx5XxE9MVDHn2RohyJHwYUNMfIipBNPZUPRA9ba0EfpGO8FDq0uxgXNixM6N2LltOo7puKbjdVjzmJrZvt68mW5+tx9ROtd/UFM8A3rWMtixBSTVPInbn6GGyGENNYHAzklV9BBwtgHuJNzsl4Pb88MW58slyxLI1DXyms/lc2t3gWGkyUBGNRbaz1VtXkZaY6OnB2bVaDRYRQ9QV4cOTueue5A0LG632+UJuyXCkUo2+5DJcydXJ7X+SfWG80JeED5nX0uWVfLb3v0j6t1x+aJScj8qUS8U5/eHYj+vz5+0h1BbX2RU21xknrynPmqvoJ29YmdTh0rI0Cedf9QLn6FEDvn6qkfUjymcc102l71IxccVTfxCimYgq0SfffqYf1Pvqdd9gTf9F1xVV2jUhajU4eEgcnEvZPz+kO1dGPg/cj6zdeKP3cedY+8pHK+NZtCVCJ/xQiGWdx+Olg8UW5sQvaCpcuO92F0cQ4wXf+9No3O+pmMdgEfe+FR8nE4Aiec21Wn2NJ92AxyeTIMfH4jM57Je5PM8Y6msrR+zYX/fmh1RWrOXQoV2ew3UYOOR1t6jPozmX1Itx9cF18DPesC/P6Yu3r+YG/hdzEWGjr+f78+1/X/p5f2o+62c+oa8+Tv6u/8DUEsHCMEmpCD0BwAA9x8AAFBLAQIUABQACAgIAHWYcENFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAdZhwQ8EmpCD0BwAA9x8AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACMCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
Version vom 16. November 2013, 19:03 Uhr
Inhaltsverzeichnis |
Faltkonstruktion der Parabel
Normalparabel
Es sei 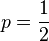 ,
, 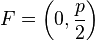 .
.
Die Gerade  sei durch die Gleichung
sei durch die Gleichung 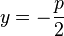 gegeben.
gegeben. 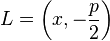 sei ein beliebiger Punkt auf
sei ein beliebiger Punkt auf  .
.
Der Punkt  sei der Schnittpunkt der Mittelsenkrechten
sei der Schnittpunkt der Mittelsenkrechten  von
von 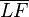 mit der in
mit der in  auf
auf  errichteten Senkrechten
errichteten Senkrechten  .
.
Aufgabe 1
Man beweise:  ist Tangente an die Normalparabel
ist Tangente an die Normalparabel 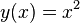 in
in  .
.
Aufgabe 2
Man beweise: 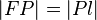 .
.
Aufgabe 3
Gegeben sei der Punkt 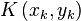 . Man beweise:
. Man beweise:
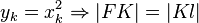
Parabel: 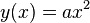
Aufgabe 4
Die Lösung der Aufgaben 2 und 3 hätte sich nicht zwangsläufig auf die Normalparabel beziehen müssen. Formulieren Sie eine Definition für den Begriff Parabel:
Definition
Parabel
Es seien  eine Gerade und
eine Gerade und  ein Punkt außerhalb von
ein Punkt außerhalb von  . Unter der Parabel mit der Leitgeraden
. Unter der Parabel mit der Leitgeraden  und dem Brennpunkt
und dem Brennpunkt  versteht man die Menge aller Punkte
versteht man die Menge aller Punkte  mit ... .
mit ... .
Aufgabe 5
Der Brennpunkt  einer Parabel mit der Funktionsgleichung
einer Parabel mit der Funktionsgleichung 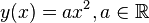 habe zur Leitgeraden
habe zur Leitgeraden  den Abstand
den Abstand  . Man drücke
. Man drücke  mittels
mittels  aus.
aus.
Aufgabe 6
Gegeben sei die Parabel  durch
durch 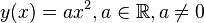 . Man beweise: ein zur y-Achse paralleler Lichtstrahl
. Man beweise: ein zur y-Achse paralleler Lichtstrahl  , der von innen auf
, der von innen auf  trifft, wird so reflektiert, dass er durch den Brennpunkt
trifft, wird so reflektiert, dass er durch den Brennpunkt  von
von  geht.
geht.
Experimentierumgebungen:
Normalparabel

