Lösung von Aufgabe 5.3 P (WS 13/14): Unterschied zwischen den Versionen
| Zeile 13: | Zeile 13: | ||
<br/>Doch die isch transitiv, weil wenn ''g'' schneidet ''h'' und ''h'' schneidet ''g'', dann ''g'' schneidet ''g''. Das gilt, weil die Relation reflexiv ist, wie Du richtig festgestellt hast. Symmetrisch isch sie auch. --[[Benutzer:Knöbelspieß|Knöbelspieß]] 22:11, 26. Nov. 2013 (CET)<br/><br /> | <br/>Doch die isch transitiv, weil wenn ''g'' schneidet ''h'' und ''h'' schneidet ''g'', dann ''g'' schneidet ''g''. Das gilt, weil die Relation reflexiv ist, wie Du richtig festgestellt hast. Symmetrisch isch sie auch. --[[Benutzer:Knöbelspieß|Knöbelspieß]] 22:11, 26. Nov. 2013 (CET)<br/><br /> | ||
Eine Relation ist nur transitiv, wenn das für alle möglichen Kombinationen gilt. Ein Gegenbeispiel (wie es Smartie nennt) genügt, um zu zeigen, dass diese Eigenschaft hier nicht gilt. <br /> | Eine Relation ist nur transitiv, wenn das für alle möglichen Kombinationen gilt. Ein Gegenbeispiel (wie es Smartie nennt) genügt, um zu zeigen, dass diese Eigenschaft hier nicht gilt. <br /> | ||
| − | Die anderen Eigenschaften sind richtig begründet.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:35, 28. Nov. 2013 (CET) | + | Die anderen Eigenschaften sind richtig begründet.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:35, 28. Nov. 2013 (CET)<br><br> |
| + | Es stimmt schon, dass ein einziges Gegenbeispiel zur Widerlegung der Eigenschaft Transitivität genügt. Nur ist dieses Gegenbeispiel an dieser Stelle m. E. unzulässig. Wir definieren eine Relation als Teilmenge des Kreuzproduktes zweier Mengen. Darin sind alle möglichen Geraden der Ebene enthalten, auch eine hypothetische Gerade ''k''. Wir betrachten auf der Relation jedoch nur die Geraden ''g'' und ''h''. Gerade ''k'' ist in dieser Teilmenge nicht enthalten, daher kann sie auch nicht zu einer möglichen Kombination herangezogen werden. --[[Benutzer:Knöbelspieß|Knöbelspieß]] 04:47, 30. Nov. 2013 (CET) | ||
Version vom 30. November 2013, 04:47 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
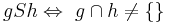
Die Relation ist reflexiv, da g sich selbst schneiden kann (g ist mit sich selbst identisch)
Die Relation ist symmetrisch, weil wenn g schneidet h dann schneidet h auch g
Die Relation ist nicht transitiv, weil wenn g schneidet h und h schneidet k nicht unbedingt g k schneiden muss, falls g und k parallel zueinander sind
--Smartie 15:48, 26. Nov. 2013 (CET)
Doch die isch transitiv, weil wenn g schneidet h und h schneidet g, dann g schneidet g. Das gilt, weil die Relation reflexiv ist, wie Du richtig festgestellt hast. Symmetrisch isch sie auch. --Knöbelspieß 22:11, 26. Nov. 2013 (CET)
Eine Relation ist nur transitiv, wenn das für alle möglichen Kombinationen gilt. Ein Gegenbeispiel (wie es Smartie nennt) genügt, um zu zeigen, dass diese Eigenschaft hier nicht gilt.
Die anderen Eigenschaften sind richtig begründet.--Tutorin Anne 11:35, 28. Nov. 2013 (CET)
Es stimmt schon, dass ein einziges Gegenbeispiel zur Widerlegung der Eigenschaft Transitivität genügt. Nur ist dieses Gegenbeispiel an dieser Stelle m. E. unzulässig. Wir definieren eine Relation als Teilmenge des Kreuzproduktes zweier Mengen. Darin sind alle möglichen Geraden der Ebene enthalten, auch eine hypothetische Gerade k. Wir betrachten auf der Relation jedoch nur die Geraden g und h. Gerade k ist in dieser Teilmenge nicht enthalten, daher kann sie auch nicht zu einer möglichen Kombination herangezogen werden. --Knöbelspieß 04:47, 30. Nov. 2013 (CET)

