Lösung von Aufgabe 11.4: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: == Versuch 1: == Satz VII.6 ist ein Kriterium. Ein Kriterium muss hinreichende und notwendige Bedingungen erfüllen. Diese Äquivalenz ist durch die jeweiligen Implika...) |
|||
| Zeile 1: | Zeile 1: | ||
| + | Begründen Sie, warum mittels der Sätze Satz VII.6 a und Satz VII.6 b der Satz VII.6 bewiesen wurde. | ||
| + | |||
| + | ===== Satz VII.6 a: (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von <math>\overline{AB}</math>gehört.) ===== | ||
| + | ::Wenn ein Punkt <math>\ P</math> zu den Endpunkten der Strecke <math>\overline{AB}</math> jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von <math>\overline{AB}</math>. | ||
| + | |||
| + | ===== Satz VII.6 b (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von <math>\overline{AB}</math> gehört)===== | ||
| + | ::Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand. | ||
| + | |||
| + | ===== Satz VII.6: (Mittelsenkrechtenkriterium) ===== | ||
| + | ::Eine Menge <math>\ M</math> von Punkten ist genau dann die Mittelsenkrechte einer Strecke <math>\ \overline{AB}</math>, wenn für jeden Punkt <math>\ P \in\ M</math> gilt: <math>\overline{AP} \cong \overline{BP}</math>. | ||
| + | |||
| + | |||
== Versuch 1: == | == Versuch 1: == | ||
Satz VII.6 ist ein Kriterium. Ein Kriterium muss hinreichende und notwendige Bedingungen erfüllen. Diese Äquivalenz ist durch die jeweiligen Implikationen (Ist das Wort richtig? Ich meine damit die "Hin"- und "Rückrichtung" des Satzes.)in den Sätzen VII.6a und VII.6b gezeigt. Somit ist auch der Satz VII.6 bewiesen.--[[Benutzer:Löwenzahn|Löwenzahn]] 11:46, 4. Jul. 2010 (UTC) | Satz VII.6 ist ein Kriterium. Ein Kriterium muss hinreichende und notwendige Bedingungen erfüllen. Diese Äquivalenz ist durch die jeweiligen Implikationen (Ist das Wort richtig? Ich meine damit die "Hin"- und "Rückrichtung" des Satzes.)in den Sätzen VII.6a und VII.6b gezeigt. Somit ist auch der Satz VII.6 bewiesen.--[[Benutzer:Löwenzahn|Löwenzahn]] 11:46, 4. Jul. 2010 (UTC) | ||
| + | |||
| + | |||
| + | == Versuch 2: == | ||
| + | (siehe Diskussion) | ||
| + | Satz VII.6 stellt eine Äquivalenzrelation dar. Satz VII.6.a ist die hinreichende Bedingung, das heißt bis wir Satz VII.6.b bewiesen hatten, konnten wir nicht sagen, ob es nicht doch Punkte gibt auf der Mittelsenkrechten, für die NICHT gilt, dass sie den selben Abstand zu den Endpunkten der Strecke gehören. | ||
| + | Das klingt nach einfacher Aussagenlogik. Bei einer Äquivalenzrelation (und nur dann) gilt: | ||
| + | <br /> aus A folgt B '''und''' aus B folgt A. | ||
| + | <br /> | ||
| + | Wenn gilt <math>A \rightarrow B </math> und <math>B \rightarrow A </math>, heißt das <math>A \leftrightarrow B </math> | ||
| + | --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 16:25, 7. Jul. 2010 (UTC) | ||
Version vom 7. Juli 2010, 17:25 Uhr
Begründen Sie, warum mittels der Sätze Satz VII.6 a und Satz VII.6 b der Satz VII.6 bewiesen wurde.
Inhaltsverzeichnis |
Satz VII.6 a: (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von  gehört.)
gehört.)
- Wenn ein Punkt
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke  jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von  .
.
- Wenn ein Punkt
Satz VII.6 b (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von  gehört)
gehört)
- Wenn ein Punkt
 zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke  gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten  und
und  ein und denselben Abstand.
ein und denselben Abstand.
- Wenn ein Punkt
Satz VII.6: (Mittelsenkrechtenkriterium)
- Eine Menge
 von Punkten ist genau dann die Mittelsenkrechte einer Strecke
von Punkten ist genau dann die Mittelsenkrechte einer Strecke  , wenn für jeden Punkt
, wenn für jeden Punkt 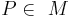 gilt:
gilt: 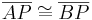 .
.
- Eine Menge
Versuch 1:
Satz VII.6 ist ein Kriterium. Ein Kriterium muss hinreichende und notwendige Bedingungen erfüllen. Diese Äquivalenz ist durch die jeweiligen Implikationen (Ist das Wort richtig? Ich meine damit die "Hin"- und "Rückrichtung" des Satzes.)in den Sätzen VII.6a und VII.6b gezeigt. Somit ist auch der Satz VII.6 bewiesen.--Löwenzahn 11:46, 4. Jul. 2010 (UTC)
Versuch 2:
(siehe Diskussion)
Satz VII.6 stellt eine Äquivalenzrelation dar. Satz VII.6.a ist die hinreichende Bedingung, das heißt bis wir Satz VII.6.b bewiesen hatten, konnten wir nicht sagen, ob es nicht doch Punkte gibt auf der Mittelsenkrechten, für die NICHT gilt, dass sie den selben Abstand zu den Endpunkten der Strecke gehören.
Das klingt nach einfacher Aussagenlogik. Bei einer Äquivalenzrelation (und nur dann) gilt:
aus A folgt B und aus B folgt A.
Wenn gilt 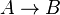 und
und 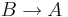 , heißt das
, heißt das 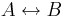 --Heinzvaneugen 16:25, 7. Jul. 2010 (UTC)
--Heinzvaneugen 16:25, 7. Jul. 2010 (UTC)

