Diskussion:Winkelmessung: Unterschied zwischen den Versionen
TimoRR (Diskussion | Beiträge) (Die Seite wurde neu angelegt: ===== Definition V.8 : (Relation senkrecht auf der Menge der Geraden) ===== :: Es seien <math>\ g</math> und <math>\ h</math> zwei Geraden. Wenn sich <math>\ g</math> u...) |
|||
| Zeile 17: | Zeile 17: | ||
korrekt --[[Benutzer:*m.g.*|*m.g.*]] 13:51, 28. Jun. 2010 (UTC) | korrekt --[[Benutzer:*m.g.*|*m.g.*]] 13:51, 28. Jun. 2010 (UTC) | ||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 16. November 2010, 22:27 Uhr
Definition V.8 : (Relation senkrecht auf der Menge der Geraden)
- Es seien
und 
zwei Geraden. Wenn sich und schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden und senkrecht aufeinader.
- Es seien
- In Zeichen:
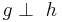(in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
- In Zeichen:
Bemerkung: Testen Sie ob die Definition korrekt ist: Warum muss nicht gefordert werden, dass die beiden Geraden komplanar sind?
Geraden sind eindimensionale Objekte. Ebenen sind zweidimensionale Objekte. Wenn Geraden komplanar sind, dann liegen alle Punkte (mindestens 2, da sonst keine Gerade) auf dieser Geraden in einer Ebene.
Da wir uns aber bei dem Schnitt zweier Geraden immer noch in einer Dimension befinden und die Geraden per Definition jeweils aus mindestens 2 verschiedenen Punkten bestehen, benötigen wir nicht die Forderung nach komplanaren Geraden.
(Beim zweiten Satz bin ich noch etwas unsicher --TimoRR 13:55, 26. Jun. 2010 (UTC)
Bemerkung --*m.g.* 13:51, 28. Jun. 2010 (UTC)
Dier Sache mit der Dimension hab ich aus rein heuristischen Gründen mit in die Vorlesung genommen: Sie sollte Analogien zwischen Halbgeraden und dem zweidimensionalen Analogon Halbebenen herstellen. Wir gebrauchen hier den Begriff der Dimension also rein intuitiv. Da wir nicht exakt geklärt haben, was eine Dimension ist, können wir zwar unsere intuitiven Vorstellungen zum Begriff der Dimension zur Findung von Beweisideen einsetzen, zum Beweisen selbst aber nicht.
Eine Definition, die festlegt, dass jede Gerade zwei verschiedene Punkte enthält, kenne ich nicht.
Oder anders ausgedrückt:
Nach Axiom I/2 enthält jede Gerade wenigstens zwei verschiedene Punkte. Seien das für die Gerade g die Punkte A und S und für die Gerade h die Punkte B und S. S sei dann der Schnittpunkt der Geraden g und h. Wir haben somit drei paarweise verschiedene Punkte. Naxch Axiom I/4 existiert damit genau eine Ebene, die diese Punkte enthält. Die Geraden g und h sind also komplanar. --Maude001 11:40, 27. Jun. 2010 (UTC)
korrekt --*m.g.* 13:51, 28. Jun. 2010 (UTC)
