Auftrag der Woche 4 (WS 16 17): Unterschied zwischen den Versionen
AlanTu (Diskussion | Beiträge) (Konstruktionsbeschreibung und zweite Lösungsmöglichkeit hinzugefügt, Diskussion auf Diskussionsseite verschoben) |
|||
| Zeile 4: | Zeile 4: | ||
<br><hr><br> | <br><hr><br> | ||
| + | |||
| + | [{{fullurl:Auftrag der Woche 4 (WS 16 17)|action=purge}} Seite neu laden, falls GeoGebra nicht lädt] | ||
| + | |||
| + | ===Lösung von AlanTu=== | ||
Wenn man den Haken bei „Spur“ setzt, erscheint nach und nach die Mittelsenkrechte. | Wenn man den Haken bei „Spur“ setzt, erscheint nach und nach die Mittelsenkrechte. | ||
<ggb_applet width="1000" height="900" version="4.0" ggbBase64="UEsDBBQACAgIAOVVcEkAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADlVXBJAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1aW2/juBV+nv0VhJ5aILZFUjcPnFk4Ayw6aGamRdJi24cuaIm2udatFOXYwf74HpKSLMW5OpntPkwQhxJ5dC7fufBQzuzHXZaiLZeVKPJzB49dB/E8LhKRr86dWi1HkfPjhx9mK16s+EIytCxkxtS542lKkZw7JPJiP0rwKCRRNPKmMR4teIRHLl+6bkxYNOWxg9CuEu/z4gvLeFWymF/Fa56xyyJmygheK1W+n0xubm7GrahxIVeT1Wox3lWJg0DNvDp3mov3wG7w0A015MR18eTnz5eW/UjklWJ5zB2kTajFhx/ezW5EnhQ36EYkan3uRCRw0JqL1RpsioLIQRNNVAIgJY+V2PIKHu3dGptVVjqGjOV6/Z29QmlnjoMSsRUJl+eOO8bTyPdCgn1vGtAgcqmDCil4rhpi3AidtOxmW8FvLF99ZUR6DlJFkS6YZol++w0Rl7joTA/YDgSGILBLrp1zqR2IHTw7+JbGs497ltSzNJ6l8UDHrajEIuXnzpKlFUAo8qUE93X3ldqn3OjTTBzMx2dgUyVugZi6ECcWc5h33TP9CeDj6YXJ0Ejck6pk/UKhrcjAJz2RPjnzaXSGMQ7PppQcySSvkUlbmTjwjs0k/gNmBo+ga3V4jp3Y70ELosyv+RxJpOQFEu396wRqOH4HE2eTNlVmTXagaq1pG08qnlU6X+gU+VMd9hj5kBtBCFHuIzyFISQIsgFhH3k+3OIIBXoMEQ1hwUMURUjTYYpMcvgR/PFCwyxAPjDTsyHkJMIgyEM+RdjklIcgk5DJS8hRQoHC95EPD2nxmGgWNEBeAHc0Qh7oqFMyxEBI4UG4B/EEUYyofhiHiAQo0Pywp1M9iLTqwJKgwEUB1gwhqyGjbTYDfYSotiZo4BJ5WasBRHGWtJeqKDtfADXUo0PZs/VpUBXfzVK24ClsFFfakwhtWaozwghaFrlCrROJnVtJVq5FXF1xpeCpCv3KtuySKb77CairVrahjYu8+pss1McirbO8QiguUrfTuUhx75p0WsMN7S14/QW/txD0rsN75RawguqKg/xCVi05S5JPmuJQGgDJr3m6v5CcbcpCDM2YTcyeM+N1nIpEsPyfEKxaisYFtVuQKVftFhR6tFWkkMnVvoIIRrt/c1lApaLR2J0SGoaRT3EQ6t1qb5c8PxiTaRAFQeAHoetOQbWY6dzz/HHgkQiqPg4wFEKQte8t+X4UhCENpzQIsZXMt52D2I4fbF1Jndi9m0/VRZEepoz5H1mpammaB6iNUhs1z1cpNyFiii3szPFmUeyubGxQy+t6X8KdazVYrAzsCEoD8X0gaMaFHQ2NVq2jcg2NayjcNthE0q3jKTEUZlzY0VBB9FrVGlNxayZ2WzGiMgXNdZq0aYuVjn290de5UJftjRLxpjEV2we+1NmCdxE05InfjqfWGnqOSv3cNHH6+l+96+s1V0x3Iz6h/jQKQx/+kmkU2UC9E6KzDZc5T5uMgGCoi7qyCd5LloTHIoNbu9BAyrS7/wEG2NmEryRvDU9NY2cBN6tuP9iPpg2rn2SRfcq31xBLRwpAdychvkAJvW/Y5RaT2aS1YVbFUpQ6otEC9pgNP8QsIMNgi0r6SasTHJjEhqUSSgP/Vzu3MXOfhVIcqPON5PFa6bpQq3UBcTZPWX5dA1soauA6024WclOtOVfXfKcQWxTbp9mB43VUGG14yjNoFZEyCWJyrAuUuZGgIwIVi1+hMHd7t10/hAcs35ssJq1YWq5NaDSwp2zP5cARht/nIrnrnhZ4qFKl6XQhPkvObWhbjeGiBIamIgzqLHi8QjsrFu1BFT3e2oi1Pbi2VVeJwcZiZ++ECsSvhekJwC7+WICdApfXwOW+EVxxkWUsT1BuOrNLqIcXogJkCukcGgbm6mBDDGsILT61ahcyy7JhdOQBXWI7gLNjBwxrX8/mh1zgnu6AA4wj707YBR2vbktQ0Kxs4ERWmX1LNTuUufiLSBJuGlW7Zf43t49Utk6LrExFLNTjsZnXGZci7my3iIO+daM1HvvBtKl0J8UsHOSOIMPPhKyhq1J9jEWZMG8HIPgzttOMgeOiguZMwVEeCnx+OMpb7ZrmBo4/GmD9CG4Qpwb6pdjxrvOE4iluYZ9hA3tO8cRxTYKzcJdm8j9/In9GE2iSe1y6fDvsHA+lx0ch45TfnxjyKDHixxMD9pme8+MnStMDiQEtne1s9LhoxlPT46TQFyueb03BgC595zYtx95tS1Q7swOMRrbY42bqFvfqF7hNih2at/TzlmpOTORB60qnbvsDcT2njYi513KeQ5M/Ii3Hu1mpzy5iKeITfHzxkI+Tl/g4+e7jx3xMGyffda3XudZ9nWs/5QraZrDjjndj690EBtL1sT0n//0X/Libh12GJj+lZvvYutklr281DjvdF/bFlF0z3trx7RqG50GK74GUvAxSchKk7fGxxdSMf3RMr/hKz9+/zTTADcCUT8Vn1XDsOo0TI/ThruK5UNJnQ/nWfZhBLNU7fRez0CYcH2o3nJf6bcTX/FqyvNLfdwwPlqA9Kw/nTXmKM7UXH2in5VOZcezM03LjuzPfyJkXbWYelzn5i/dSZ3rfnfn/zUxs3Tm/x5n0pc6k3535rZzJd6UEZTXBoe+6KmvpIFhqHDnoJZ56ndY+/+wmHbr7RNjDpv4eoKFm37azU5LF/AiqBx396tdp98BMBjCTF8NMvhHMb9rt/d44DxBbFEXKWd6hwe6+Guq/BH/F68zn15avy2XFlX2RYwz3yWPoDXLXuPuOvZP+a3bzVVnzbx8f/gdQSwcIgJS+GDIIAACTIgAAUEsBAhQAFAAICAgA5VVwSUXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADlVXBJgJS+GDIIAACTIgAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMoIAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="1000" height="900" version="4.0" ggbBase64="UEsDBBQACAgIAOVVcEkAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADlVXBJAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1aW2/juBV+nv0VhJ5aILZFUjcPnFk4Ayw6aGamRdJi24cuaIm2udatFOXYwf74HpKSLMW5OpntPkwQhxJ5dC7fufBQzuzHXZaiLZeVKPJzB49dB/E8LhKRr86dWi1HkfPjhx9mK16s+EIytCxkxtS542lKkZw7JPJiP0rwKCRRNPKmMR4teIRHLl+6bkxYNOWxg9CuEu/z4gvLeFWymF/Fa56xyyJmygheK1W+n0xubm7GrahxIVeT1Wox3lWJg0DNvDp3mov3wG7w0A015MR18eTnz5eW/UjklWJ5zB2kTajFhx/ezW5EnhQ36EYkan3uRCRw0JqL1RpsioLIQRNNVAIgJY+V2PIKHu3dGptVVjqGjOV6/Z29QmlnjoMSsRUJl+eOO8bTyPdCgn1vGtAgcqmDCil4rhpi3AidtOxmW8FvLF99ZUR6DlJFkS6YZol++w0Rl7joTA/YDgSGILBLrp1zqR2IHTw7+JbGs497ltSzNJ6l8UDHrajEIuXnzpKlFUAo8qUE93X3ldqn3OjTTBzMx2dgUyVugZi6ECcWc5h33TP9CeDj6YXJ0Ejck6pk/UKhrcjAJz2RPjnzaXSGMQ7PppQcySSvkUlbmTjwjs0k/gNmBo+ga3V4jp3Y70ELosyv+RxJpOQFEu396wRqOH4HE2eTNlVmTXagaq1pG08qnlU6X+gU+VMd9hj5kBtBCFHuIzyFISQIsgFhH3k+3OIIBXoMEQ1hwUMURUjTYYpMcvgR/PFCwyxAPjDTsyHkJMIgyEM+RdjklIcgk5DJS8hRQoHC95EPD2nxmGgWNEBeAHc0Qh7oqFMyxEBI4UG4B/EEUYyofhiHiAQo0Pywp1M9iLTqwJKgwEUB1gwhqyGjbTYDfYSotiZo4BJ5WasBRHGWtJeqKDtfADXUo0PZs/VpUBXfzVK24ClsFFfakwhtWaozwghaFrlCrROJnVtJVq5FXF1xpeCpCv3KtuySKb77CairVrahjYu8+pss1McirbO8QiguUrfTuUhx75p0WsMN7S14/QW/txD0rsN75RawguqKg/xCVi05S5JPmuJQGgDJr3m6v5CcbcpCDM2YTcyeM+N1nIpEsPyfEKxaisYFtVuQKVftFhR6tFWkkMnVvoIIRrt/c1lApaLR2J0SGoaRT3EQ6t1qb5c8PxiTaRAFQeAHoetOQbWY6dzz/HHgkQiqPg4wFEKQte8t+X4UhCENpzQIsZXMt52D2I4fbF1Jndi9m0/VRZEepoz5H1mpammaB6iNUhs1z1cpNyFiii3szPFmUeyubGxQy+t6X8KdazVYrAzsCEoD8X0gaMaFHQ2NVq2jcg2NayjcNthE0q3jKTEUZlzY0VBB9FrVGlNxayZ2WzGiMgXNdZq0aYuVjn290de5UJftjRLxpjEV2we+1NmCdxE05InfjqfWGnqOSv3cNHH6+l+96+s1V0x3Iz6h/jQKQx/+kmkU2UC9E6KzDZc5T5uMgGCoi7qyCd5LloTHIoNbu9BAyrS7/wEG2NmEryRvDU9NY2cBN6tuP9iPpg2rn2SRfcq31xBLRwpAdychvkAJvW/Y5RaT2aS1YVbFUpQ6otEC9pgNP8QsIMNgi0r6SasTHJjEhqUSSgP/Vzu3MXOfhVIcqPON5PFa6bpQq3UBcTZPWX5dA1soauA6024WclOtOVfXfKcQWxTbp9mB43VUGG14yjNoFZEyCWJyrAuUuZGgIwIVi1+hMHd7t10/hAcs35ssJq1YWq5NaDSwp2zP5cARht/nIrnrnhZ4qFKl6XQhPkvObWhbjeGiBIamIgzqLHi8QjsrFu1BFT3e2oi1Pbi2VVeJwcZiZ++ECsSvhekJwC7+WICdApfXwOW+EVxxkWUsT1BuOrNLqIcXogJkCukcGgbm6mBDDGsILT61ahcyy7JhdOQBXWI7gLNjBwxrX8/mh1zgnu6AA4wj707YBR2vbktQ0Kxs4ERWmX1LNTuUufiLSBJuGlW7Zf43t49Utk6LrExFLNTjsZnXGZci7my3iIO+daM1HvvBtKl0J8UsHOSOIMPPhKyhq1J9jEWZMG8HIPgzttOMgeOiguZMwVEeCnx+OMpb7ZrmBo4/GmD9CG4Qpwb6pdjxrvOE4iluYZ9hA3tO8cRxTYKzcJdm8j9/In9GE2iSe1y6fDvsHA+lx0ch45TfnxjyKDHixxMD9pme8+MnStMDiQEtne1s9LhoxlPT46TQFyueb03BgC595zYtx95tS1Q7swOMRrbY42bqFvfqF7hNih2at/TzlmpOTORB60qnbvsDcT2njYi513KeQ5M/Ii3Hu1mpzy5iKeITfHzxkI+Tl/g4+e7jx3xMGyffda3XudZ9nWs/5QraZrDjjndj690EBtL1sT0n//0X/Libh12GJj+lZvvYutklr281DjvdF/bFlF0z3trx7RqG50GK74GUvAxSchKk7fGxxdSMf3RMr/hKz9+/zTTADcCUT8Vn1XDsOo0TI/ThruK5UNJnQ/nWfZhBLNU7fRez0CYcH2o3nJf6bcTX/FqyvNLfdwwPlqA9Kw/nTXmKM7UXH2in5VOZcezM03LjuzPfyJkXbWYelzn5i/dSZ3rfnfn/zUxs3Tm/x5n0pc6k3535rZzJd6UEZTXBoe+6KmvpIFhqHDnoJZ56ndY+/+wmHbr7RNjDpv4eoKFm37azU5LF/AiqBx396tdp98BMBjCTF8NMvhHMb9rt/d44DxBbFEXKWd6hwe6+Guq/BH/F68zn15avy2XFlX2RYwz3yWPoDXLXuPuOvZP+a3bzVVnzbx8f/gdQSwcIgJS+GDIIAACTIgAAUEsBAhQAFAAICAgA5VVwSUXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADlVXBJgJS+GDIIAACTIgAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMoIAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| − | |||
| − | + | ||
| − | + | ====Konstruktionsbeschreibung==== | |
| − | + | Gegeben seien zwei Punkte <math>A</math> und <math>B</math>. Gesucht ist <math>M:=\{Q|\overline{AQ}\cong\overline{QB}\}</math>. | |
| − | + | ||
| − | + | Sei <math>r\in\mathbb{R}</math> fest aber beliebig. | |
| − | + | # Zeichne einen Kreis <math>c_r</math> mit Radius <math>r</math> um <math>A</math> (die Menge der Punkte mit Abstand <math>r</math> von <math>A</math>). | |
| − | + | # Zeichne einen Kreis <math>d_r</math> mit Radius <math>r</math> um <math>B</math> (die Menge der Punkte mit Abstand <math>r</math> von <math>B</math>). | |
| − | + | # Bestimme <math>M_r</math> (die Menge der Punkte mit Abstand <math>r</math> sowohl von <math>A</math> als auch von <math>B</math>) folgendermaßen: | |
| + | ## Falls kein Schnittpunkt von <math>c</math> und <math>d</math>: Es sei <math>M_r=\{\}</math>. | ||
| + | ## Falls ein Schnittpunkt von <math>c</math> und <math>d</math>: Nenne den Schnittpunkt <math>Q</math>, es sei <math>M_r=\{Q\}</math>. | ||
| + | ## Falls zwei Schnittpunkte von <math>c</math> und <math>d</math>: Nenne die beiden Schnittpunkte <math>Q_r^1</math> und <math>Q_r^2</math>, es sei <math>M_r=\{Q_r^1,Q_r^2\}</math>. | ||
| + | |||
| + | <math>M</math> ergibt sich nun aus der Vereinigung aller <math>M_r</math> für <math>r\in\mathbb{R}</math>, also: <math>M = \bigcup\limits_{r\in\mathbb{R}}{M_r}</math> | ||
| + | |||
| + | ====Begründung, warum die Menge genau die Mittelsenkrechte ist==== | ||
| + | |||
| + | Betrachtet man nun <math>r=\frac{\overline{AB}}{2}</math>: <math>Q</math> ist der Mittelpunkt von <math>A</math> und <math>B</math>, da er den selben Abstand von beiden Punkten hat. | ||
| + | |||
| + | Betrachtet man nun <math>r\in\mathbb{R} \wedge r > \overline{QA}</math>: | ||
| + | * Das Viereck <math>AQ_r^1BQ_r^2</math> bildet eine Raute mit Seitenlänge <math>r</math>. | ||
| + | * Da die Diagonalen der Raute sich sowohl halbieren, als auch senkrecht aufeinander stehen, liegen <math>Q_r^1</math> und <math>Q_r^2</math> auf der Mittelsenkrechten von <math>A</math> und <math>B</math>. | ||
| + | * Nach dem Satz des Pythagoras ergibt sich <math>\overline{QQ_r^1} = \overline{QQ_r^2} = \sqrt{r^2 - \overline{QA}^2}</math> und da <math>f(r)=\sqrt{r^2 - \overline{QA}^2}</math> für <math>r > \overline{QA}</math> genau einen Wertebereich von <math>(0,\infty)</math> besitzt, ergibt die Vereinigung aller <math>M_r</math> genau die Mittelsenkrechte von <math>A</math> und <math>B</math> ohne den Mittelpunkt von <math>A</math> und <math>B</math>. | ||
| + | |||
| + | Nimmt man also beide Fälle zusammen ergibt sich genau die komplette Mittelsenkrechte von <math>A</math> und <math>B</math>. | ||
| + | |||
| + | |||
| + | ===Lösung von Tutor Alex=== | ||
<ggb_applet id="NhGHgeYj" width="1890" height="880" border="000000" /> | <ggb_applet id="NhGHgeYj" width="1890" height="880" border="000000" /> | ||
| + | Nachtrag: Falls die GeoGebra Datei hier nicht angezeigt wird, [https://ggbm.at/uFGVcdT3 klicke hier]. | ||
| + | |||
| + | |||
| + | ===2. Lösung von AlanTu=== | ||
| + | <ggb_applet width="900" height="900" version="4.0" ggbBase64="UEsDBBQACAgIAHNacUkAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAHNacUkAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VrrbttGFv6dPsVAP4rdwpLmTjKVUzgFig2QNk2cLbq7WARDciSzpkiGpGwp275Tk0foA+SZemaGpCjJ8i12NrsIYJsczpnLuXzfOUN68s1ynqIzXVZJnh0OyAgPkM6iPE6y2eFgUU+H/uCbR19MZjqf6bBUaJqXc1UfDriRTOLDQeCHOvJFNNRx5A25lMHQDzAdChoxjZk3DTgdILSskodZ/oOa66pQkT6OTvRcPc0jVduFT+q6eDgen5+fj9qlRnk5G89m4WhZxQME28yqw0Fz8xCm2xh0zqw4xZiMf/7+qZt+mGRVrbJID5BRYZE8+uLB5DzJ4vwcnSdxfQIKEwy7O9HJ7ASU8kxjbKQKsEihozo50xWM7TWt0vW8GFgxlZn+B+4OpZ0+AxQnZ0msy8MBHpEAC0klYZxhQj3MBygvE53VjTBpFh23003OEn3u5jV3dkkYVOd5GiozJfr1V0QxxejAXIi7ULhI6bqwe4aZu1B34e4inAx3w7kT5U6GOxnOBugsqZIw1YeDqUorsGGSTUvwX9eu6lWq7X6aB2v1yQHoVCVvQJgGECjO6PAc4wPzK+GXY+z07ilJeqvW5eKGi7ZL+j69/pL0Q5ZknZbkAi2p2KOlvMS4bg/XUZOI3pqwlP2xvzsrMnoTd7otXLAil2y9IqP8gPviQIrgQFBvZ03JP4qWk3ELlkmDD1SdGNnGmbWeVwYxLEAiMIFPkAB0SA/iXCASwMWjCPCAiEBcQJP4SJqrh5gHHRwx5CMjRxiy8BA+/OGenUwiAZOZpx6gEhFYiCPBELGo4giwhCwyAaWUgYQQSMAgszyhZgomEZfQYj7isEcDSo+AIIOB0IblKWIEMTOYeIhKJM18hBuwS99sHaakSGIkiZkQcA2YdngGeR8xo41szJVkxaLeMFE0j9vbOi86X4A0MNKa+BxDbfDig0mqQp1Crjg2nkToTKUGFHahaZ7VqHUidc9mpSpOkqg61nUNoyr0izpTT1Wtl9+BdNWubWWjPKt+LPP62zxdzLMKoShPcbfnPCW9e9q7Z7173mkDDdHrkP0Or+nYWDaHDrSoNCyfl1U7VMXxEyPRRTDY8VmWrh6XWp0WebKpxGRsk85EL6I0iROV/QShahYxVkFtDrJ01aYg4XntPvIyPl5VEL9o+U9d5iZZQX6WnieIZJ5PuADQrVyXpN6IBgGjRPqe5D7sLFIGeAEZcRkElFHKiM89AOVqT5dwC+uzzjtqqTt10Kw0qO41nlSP83T9yGr/rSrqRWmLB6CK0uh0lM1SbePDki1k5ug0zJfHLjCYm+vlqoAWdjsIZ9boCHiBCgECzTV0VytjttZJYSuDrQRuIy2Ju34SUCthr6G7WikIXbe1RlXSqklwu0xSWTbDgwYzLVOZwDd5fpEl9dO2USfRaaMqcQN+WMxD3cXP5pzk7uY0u4aSo6p/boo4c/+P3v3LE10rU4wIykTgQxDBXxr4vovTrQidnOoy02mDBwiGRb6oHLp7CI11lMyh6Toakyrj7r+DAu5prGelbhVPbWHnDG57cT/Wdx7bqb4r8/mT7OwlxNLOBqC6KyG+YBMmabju1iaTcavDpIrKpDARjUJIMKd6HbNgGQX5Ke5j1sAbJonslHVSG8MD8Bf1SQ6hdJSq7OUCRgJpwXMD7lTPoZZDtQ1hi4LOlUe2SjQ+Q3n4C/Bml1xd/9qB0H1hONvAV2lxYp3XGCZVK11umMrO930ebxuwNQ3QSGFLUYigQmsXfG7HcFPAhBazG/QLPqnQsomhFWzFXN+4tiuSja4Gxxu8755uORMizJnpCoM9/rQMdhtz8cZc5I7MFeXzucpilNnC6VjPzPPBOpUrbOIMKWKs50yzqNuO0M3WzLFj/KqZrTVveIX5ewrvsz++vfV3Q441Nhx63VwdY9dQSJzCeamyaaVuEoi9+VsSx9oWkS6jvc7ckMrRaDIv0iRK6s5aqXHnk6wGUtUW97tcd6p1YZLUs+xlqbLKHIO3+WZfhFsa60z4/q21MYxdNNrTEYOcTeAgJj3qU94ERpWa8yOaJ6AI/uqP3wdoroxpfNdQYQWFUQ0naeDXbH2Sdv5qSguGjROMRalsTMqtTafJskeDwGzJG+B5tYGw26GQ4N04INeMA3J7H6sy6kFrP/9Z2zWYxiOKhggeoq+gTs3+8v7tXy9C+VrbsKvy9vt+E64vcjjk6y20PnZohUhAihrwbqP28ZeqyKuvL8fuFnE2Q3Yct1lb3DN/rhE8hEoDQ6kBlYZkTAhujoMm/EaeTyUOAi4o9jjUIfdAkrbkvNjoR87mPQtvWP7921fkcrNvoxnkr4nnO4OTKelWoGkSObGmYVw4YkHXDvudMPDJ9F/v36Iv0/prFOA/fj+AyKfw59/2DJSXx+a9XM+/HxuraZqfv9DTVC+t+zYRBiQ+B+3NuelFd6jYIun98fAUNrknY+6JA3V5EBitO/epTyRpDukF2ALIDckFUATMCRD3GPV4AFdfePeTYG/IjY1fhi057pY0Rzcnx6NPjBzlyPfg+G6OX3AUDShv6mtGOVCGDDCTXAr2saixNU9TQ+5JSkB19IbUSD9T4/1RY49W7pobN+NhOxCiG3Bj9F/lxn312uZRYxd1K0ummxhl0p1E6IhTjzLPA+qUAkaJj82b3UFly23KOSzacdjzm3Dl81udwE1KmblL6C736TMK8ARfUexjnwnIacz6DI8CQinkORIw84YUO5cFo8DH1BAOB87xiLxDOv0xT1ezPNt3HLdU+nzHIT8lMF90SpzYayemXpk2g0P4VSVo0SzauqSb7rZxeGN8EmNx8Lcgtz7rXfFaaPvNxOvbEcklG/38cuIiO6vmPPNJWBoAjX0RMA8wTSWQrt8WtIEMBCMU6Bn7Hpe+cwQZScl9bj6OBAHQA/f/b/wSfkp+MQ7Y4xjMMLgDDh8YuFiY785vDFI2/cXvKWfei1+urp+fb75a2K2c393wpcK73ZcKeOQJFvgU6hBfEiEwv37pHOVZnLjXYOZzZSNsCt5ZU/D+T7zMu9MXBJv2D/M81WqdUY+LRbntgf53pw/4PnF9AD6bTitd24zj4NV+Gr4qk17jxHdFgQIReLOz3rvds95WxPIg+ByxHxSxy6KErRijtKX6q/+YQP1tgKDP0tBGQT++qtJvh187r1zsFguW+3ttUpdw+L7kLHBByrFnAWhxLCkn1GOepITeyduUcf/zsP0Pj+bfFR/9CVBLBwhwZstJeQkAAEspAABQSwECFAAUAAgICABzWnFJ1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAHNacUlwZstJeQkAAEspAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAEAoAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "true" useBrowserForJS = "false" allowRescaling = "true" /> | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 17. November 2016, 13:56 Uhr
[ www.ph-heidelberg.de is not an authorized iframe site ]
Die Lösung ist korrekt, die Skizze aus didaktischer Sicht suboptimal. Generieren Sie mit Geogebra eine dynamische Applikation, die die korrekte Lösung besser als die obige Skizze unterstützt.
Seite neu laden, falls GeoGebra nicht lädt
Inhaltsverzeichnis |
Lösung von AlanTu
Wenn man den Haken bei „Spur“ setzt, erscheint nach und nach die Mittelsenkrechte.
Konstruktionsbeschreibung
Gegeben seien zwei Punkte  und
und  . Gesucht ist
. Gesucht ist 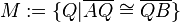 .
.
Sei 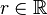 fest aber beliebig.
fest aber beliebig.
- Zeichne einen Kreis
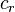 mit Radius
mit Radius  um
um  (die Menge der Punkte mit Abstand
(die Menge der Punkte mit Abstand  von
von  ).
).
- Zeichne einen Kreis
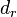 mit Radius
mit Radius  um
um  (die Menge der Punkte mit Abstand
(die Menge der Punkte mit Abstand  von
von  ).
).
- Bestimme
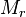 (die Menge der Punkte mit Abstand
(die Menge der Punkte mit Abstand  sowohl von
sowohl von  als auch von
als auch von  ) folgendermaßen:
) folgendermaßen:
- Falls kein Schnittpunkt von
 und
und  : Es sei
: Es sei 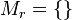 .
.
- Falls ein Schnittpunkt von
 und
und  : Nenne den Schnittpunkt
: Nenne den Schnittpunkt  , es sei
, es sei 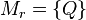 .
.
- Falls zwei Schnittpunkte von
 und
und  : Nenne die beiden Schnittpunkte
: Nenne die beiden Schnittpunkte 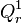 und
und 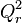 , es sei
, es sei 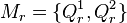 .
.
- Falls kein Schnittpunkt von
 ergibt sich nun aus der Vereinigung aller
ergibt sich nun aus der Vereinigung aller 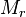 für
für 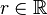 , also:
, also: 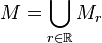
Begründung, warum die Menge genau die Mittelsenkrechte ist
Betrachtet man nun 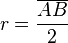 :
:  ist der Mittelpunkt von
ist der Mittelpunkt von  und
und  , da er den selben Abstand von beiden Punkten hat.
, da er den selben Abstand von beiden Punkten hat.
Betrachtet man nun 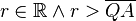 :
:
- Das Viereck
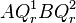 bildet eine Raute mit Seitenlänge
bildet eine Raute mit Seitenlänge  .
.
- Da die Diagonalen der Raute sich sowohl halbieren, als auch senkrecht aufeinander stehen, liegen
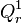 und
und 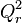 auf der Mittelsenkrechten von
auf der Mittelsenkrechten von  und
und  .
.
- Nach dem Satz des Pythagoras ergibt sich
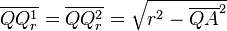 und da
und da 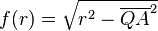 für
für 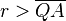 genau einen Wertebereich von
genau einen Wertebereich von 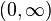 besitzt, ergibt die Vereinigung aller
besitzt, ergibt die Vereinigung aller 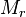 genau die Mittelsenkrechte von
genau die Mittelsenkrechte von  und
und  ohne den Mittelpunkt von
ohne den Mittelpunkt von  und
und  .
.
Nimmt man also beide Fälle zusammen ergibt sich genau die komplette Mittelsenkrechte von  und
und  .
.
Lösung von Tutor Alex
Nachtrag: Falls die GeoGebra Datei hier nicht angezeigt wird, klicke hier.
2. Lösung von AlanTu

