Lösung von Aufgabe 1.5 Algebra SoSe 2017: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 26: Zeile 26:
 
(VII) also <math>(g^{-1})^{-1}\cdot g^{-1}=e</math> <br />
 
(VII) also <math>(g^{-1})^{-1}\cdot g^{-1}=e</math> <br />
 
(IX) und damit <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}=e</math> <br />
 
(IX) und damit <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}=e</math> <br />
−
(X) oder einfach: <math>g \cdot g^{-1}=e</math> und damit: Das Linksinverse <math>g^{-1}</math> von <math>g</math> ist auch sein
+
(X) oder einfach: <math>g \cdot g^{-1}=e</math> und damit: Das Linksinverse <math>g^{-1}</math> von <math>g</math> ist auch sein Rechtsinverses.

Version vom 15. Mai 2017, 11:14 Uhr

Aufgabe 1.5 Algebra SoSe 2017

Beweisen Sie: In jeder Gruppe gilt: Das Linksinverse Element eines Gruppenelements g ist gleich dem Rechtsinversen von g.

Lösung Aufgabe 1.5 Algebra SoSe 2017

Übungsaufgabe, Hinweise

  1. Beginnen Sie mit Linksinvers=Rechtsinvers
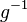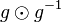
  2. Multiplizieren Sie zunächst das Linksinverse g^{-1} eines beliebigen Elementes g von rechts mit g:g \odot g^{-1}
  3. Ersetzen Sie g durch e \odot g
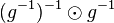  4. Ersetzen Sie e durch das Produkt des Linksinversen vom Linksinversen von g mit dem Linksinversen von g: (g^{-1})^{-1} \odot g^{-1}.
  5. Der Rest ist geschicktes Klammern und Ausnutzung der Assoziativität...

Beweis:

Es sei 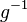g^{-1} das Linksinverse von g.

Wir muliplizieren 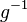g^{-1} von rechts mit g:
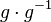
(I) g \cdot g^{-1}
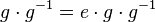
(II) g \cdot g^{-1}= e \cdot g \cdot g^{-1}
Wissen: Auch 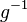g^{-1} hat ein Linksinverses: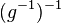 (g^{-1})^{-1}
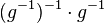
Ersetzen e durch (g^{-1})^{-1}\cdot g^{-1}

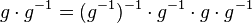
(III) g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1} \cdot g \cdot g^{-1}
(IV) geschicktes Klammern: 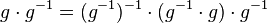g \cdot g^{-1}= (g^{-1})^{-1}\cdot (g^{-1} \cdot g) \cdot g^{-1}
(V) Klammer berechnen: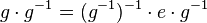g \cdot g^{-1}= (g^{-1})^{-1}\cdot e \cdot g^{-1}
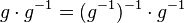
(VI) Mit e multiplizieren ist geschenkt ... g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}
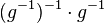(VII) (g^{-1})^{-1}\cdot g^{-1} bedeutet, das Linksinverse vom Linksinversen von g mieinander multiplizieren.
(VII) also 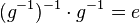(g^{-1})^{-1}\cdot g^{-1}=e
(IX) und damit 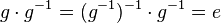g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}=e
(X) oder einfach: 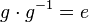g \cdot g^{-1}=e und damit: Das Linksinverse 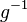g^{-1} von g ist auch sein Rechtsinverses.

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_1.5_Algebra_SoSe_2017&oldid=29742“