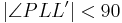Lösung von Aufgabe 12.4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 14: | Zeile 14: | ||
! style="background: #FFDDDD;"|(I) | ! style="background: #FFDDDD;"|(I) | ||
| Es existiert ein Dreieck <math>\overline {PLL'}</math> | | Es existiert ein Dreieck <math>\overline {PLL'}</math> | ||
| − | | VSS, Punkte <math>\ L L' P </math> sind nicht kollinear | + | | VSS, Punkte <math>\ L L' P </math> sind nicht kollinear, da <math>\ L \in g \and L' \in g \and P \notin g</math> laut Definition Lot und Lotfußpunkt. |
|- | |- | ||
! style="background: #FFDDDD;"|(II) | ! style="background: #FFDDDD;"|(II) | ||
| <math>|\angle LL'P| = 90</math> | | <math>|\angle LL'P| = 90</math> | ||
| − | | | + | | Annahme, <math>\ L'</math> ist Lotfußpunkt |
|- | |- | ||
! style="background: #FFDDDD;"|(III) | ! style="background: #FFDDDD;"|(III) | ||
Version vom 13. Juli 2010, 00:24 Uhr
Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt  auf eine Gerade
auf eine Gerade  .
.
Existenz
Eindeutigkeit
Voraussetzung: Gerade  , Punkt
, Punkt 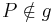 , Lot
, Lot 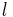 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Behauptung: Es existiert genau ein Lot von  auf
auf  .
.
Indirekter Beweis - Annahme: Es existieren zwei "Lote" von  auf
auf  .
.
Annahme: Es existiert ein zweiter Lotfußpunkt 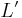
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Dreieck 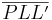
|
VSS, Punkte 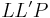 sind nicht kollinear, da sind nicht kollinear, da 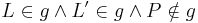 laut Definition Lot und Lotfußpunkt. laut Definition Lot und Lotfußpunkt.
|
| (II) | 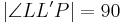
|
Annahme, 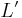 ist Lotfußpunkt ist Lotfußpunkt
|
| (III) | 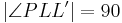
|
VSS,  ist Lotfußpunkt ist Lotfußpunkt
|
| (IV) | Außenwinkel von 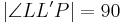
|
Supplementaxiom |
| (V) | 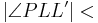 Außenwinkel von Außenwinkel von 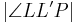
|
Schwacher Außenwinkelsatz |
| (VI) | Annahme muss verworfen werden | Widerspruch zwischen (V) und (III) !!! |