Untergruppen, Untergruppenkriterien: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Beispiel 1) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 1) |
||
| Zeile 7: | Zeile 7: | ||
Die Gruppe besteht aus den folgenden Restklassen: <math>\mathbb{Z}_6=\{ \overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4}, \overline{5} \}</math><br /> | Die Gruppe besteht aus den folgenden Restklassen: <math>\mathbb{Z}_6=\{ \overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4}, \overline{5} \}</math><br /> | ||
Die Gruppentafel sieht wie folgt aus: | Die Gruppentafel sieht wie folgt aus: | ||
| − | {| | + | {| border="1" cellspacing="0" cellpadding="20" |
|- | |- | ||
| <math>\oplus</math> || <math> \overline{0} </math> || <math> \overline{1} </math> || <math> \overline{2} </math> || <math> \overline{3} </math> || <math> \overline{4} </math> || <math> \overline{5} </math> | | <math>\oplus</math> || <math> \overline{0} </math> || <math> \overline{1} </math> || <math> \overline{2} </math> || <math> \overline{3} </math> || <math> \overline{4} </math> || <math> \overline{5} </math> | ||
Version vom 11. Dezember 2017, 17:28 Uhr
Beispiele, GegenbeispieleBeispiel 1Wir gehen von der additiven Gruppe der Restklassen modulo 6 aus
Wir wählen aus |
![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) .
.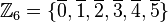




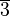
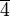
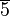
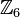 die folgenden Elemente aus:
die folgenden Elemente aus:

