Die Umkehrung des Stufenwinkelsatzes: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)) |
*m.g.* (Diskussion | Beiträge) (→Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)) |
||
| Zeile 42: | Zeile 42: | ||
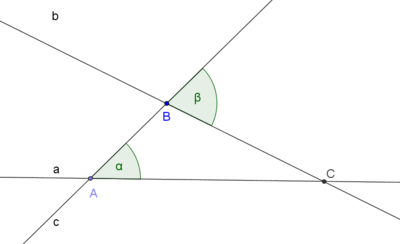
Unter Berücksichtigung von <math>a \not\equiv b</math> hätten die beiden Geraden <math>\ a</math> und <math>\ b</math> entsprechend der Annahme genau einen Punkt <math>\ C</math> gemeinsam. | Unter Berücksichtigung von <math>a \not\equiv b</math> hätten die beiden Geraden <math>\ a</math> und <math>\ b</math> entsprechend der Annahme genau einen Punkt <math>\ C</math> gemeinsam. | ||
| − | [[Bild:Umkehrung_stufenwinkelsatz_02.png| | + | [[Bild:Umkehrung_stufenwinkelsatz_02.png|400 px]] |
Bezüglich des Dreiecks <math>\overline{ABC}</math> ist <math>\ \beta</math> nun ein Außenwinkel. | Bezüglich des Dreiecks <math>\overline{ABC}</math> ist <math>\ \beta</math> nun ein Außenwinkel. | ||
| + | |||
| + | Der Winkel <math>\ \alpha</math> ist bezüglich <math>\ \beta</math> ein nichtanliegender Innenwinkel des Dreiecks <math>\overline{ABC}</math>. | ||
Version vom 14. Juli 2010, 14:35 Uhr
Inhaltsverzeichnis |
Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel
In welchen Fällen handelt es sich um....
- Stufenwinkel
- Wechselwinkel
- entgegengesetzt liegende Winkel?
Definition X.1: (Stufenwinkel)
Definition X.2: (Wechselwinkel)
Definition X.3: (entgegengesetzt liegende Winkel)
Die Umkehrung des Stufenwinkelsatzes
Satz X.1: (Umkehrung des Stufenwinkelsatzes)
- Es seien
und 
zwei nicht identische Geraden, die durch eine dritte Gerade 
jeweils geschnitten werden. Es seien ferner 
und 
zwei Stufenwinkel, die bei dem Schnitt von mit und entstehen mögen.
- Wenn die beiden Stufenwinkel und kongruent zueinander sind, dann sind die Geraden und parallel zueinander.
- Es seien
Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)
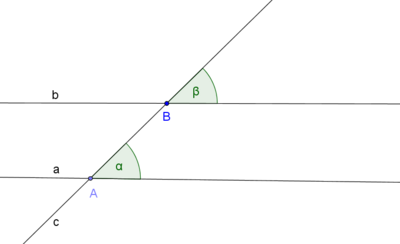
Es seien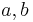 
und drei paarweise nicht identische Geraden. Die Gerade möge in dem Punkt
und die Gerade in dem Punkt 
schneiden. und sei ein Paar von Stufenwinkeln , welches bei dem Schnitt von und mit entstehen möge.
Voraussetzung:
(i)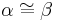 
Behauptung:
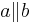
Annahme:
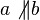
Unter Berücksichtigung von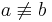 
hätten die beiden Geraden und entsprechend der Annahme genau einen Punkt 
gemeinsam.
Bezüglich des Dreiecks 
ist nun ein Außenwinkel.
Der Winkel ist bezüglich ein nichtanliegender Innenwinkel des Dreiecks .
