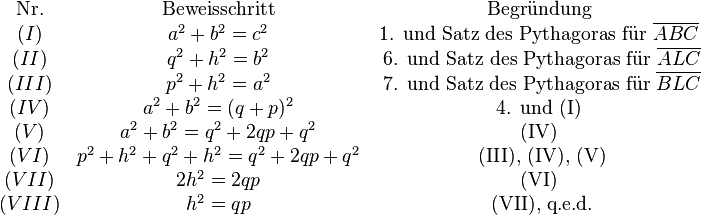Lösung von Aufgabe 2.8 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Lösung) |
*m.g.* (Diskussion | Beiträge) (→Lösung) |
||
| Zeile 24: | Zeile 24: | ||
(I) & a^2+b^2=c^2 & \text{1. und Satz des Pythagoras für } \overline{ABC} \\ | (I) & a^2+b^2=c^2 & \text{1. und Satz des Pythagoras für } \overline{ABC} \\ | ||
(II) & q^2 + h^2 = b^2 & \text{ 6. und Satz des Pythagoras für } \overline{ALC} \\ | (II) & q^2 + h^2 = b^2 & \text{ 6. und Satz des Pythagoras für } \overline{ALC} \\ | ||
| − | (III) & | + | (III) & p^2 + h^2 = a^2 & \text{ 7. und Satz des Pythagoras für } \overline{BLC} \\ |
(IV) & a^2+b^2=(q+p)^2 & \text{4. und (I)} \\ | (IV) & a^2+b^2=(q+p)^2 & \text{4. und (I)} \\ | ||
| + | (V) & a^2 + b^2 = q^2 +2qp + q^2 & \text{(IV)} \\ | ||
| + | (VI) & p^2 + h^2 + q^2 + h^2 = q^2 +2qp + q^2 & \text{ (III), (IV), (V)} \\ | ||
| + | (VII) & 2h^2 = 2qp & \text{(VI)} \\ | ||
| + | (VIII) & h^2 = qp & \text{ (VII), q.e.d.} \\ | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
Version vom 22. Mai 2018, 12:21 Uhr
Aufgabe 2.8 SoSe 2018Der Höhensatz für rechtwinklige Dreiecke lautet:
Kurz: Beweisen Sie den Höhensatz unter Verwendung des Satzes von Pythagoras. Lösung
|
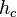 auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten
auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten 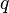 und
und  entsprechen.
entsprechen. 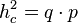
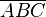 ein rechtwinkliges Dreieck mit dem rechten Winkel
ein rechtwinkliges Dreieck mit dem rechten Winkel 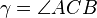 .
.
 von
von  auf die Seite
auf die Seite 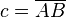 habe auf
habe auf  den Fußpunkt
den Fußpunkt 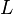 .
.
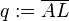 und
und 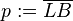 .
.
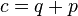 .
.
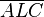 und
und 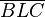 .
.
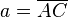 die Hypotenuse und
die Hypotenuse und 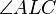 der rechte Winkel.
der rechte Winkel.
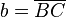 die Hypotenuse und
die Hypotenuse und 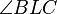 der rechte Winkel.
der rechte Winkel.