Untergruppen, Untergruppenkriterien: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Einselement) |
*m.g.* (Diskussion | Beiträge) (→Einselement) |
||
| Zeile 79: | Zeile 79: | ||
<math>\forall P \in \varepsilon : \beta \circ \operatorname{id}(P)= \operatorname{id}(\beta(P))=\beta(P)</math> und somit <math>\operatorname{id} \circ \beta = \beta</math>. | <math>\forall P \in \varepsilon : \beta \circ \operatorname{id}(P)= \operatorname{id}(\beta(P))=\beta(P)</math> und somit <math>\operatorname{id} \circ \beta = \beta</math>. | ||
| − | + | ====inverse Elemente==== | |
| + | Es genügt zu zeigen, dass jede Bewegung <math>\beta</math> eineindeutig ist, d.h. dass jeder Punkt <math>\R \in \varepsilon</math> bei <math>\beta</math> ein und nur ein Urbild <math>Q \in \varepsilon </math> hat.<br /> | ||
| + | =====Injektivität von <math>\beta</math>===== | ||
| + | Sei <math>P'</math> das Bild von <math>P</math> bei der Bewegung <math>\beta</math>. Wir haben zu zeigen, dass es keinen Punkt <math>Q \in \varepsilon, Q \not \equiv P</math> gibt, der durch <math>\beta</math> auch auf <math>P'</math> abgebildet wird. Wir nahemen, an, dass es einen solchen Punkt <math>Q</math> gibt. Dann gilt:<br /> | ||
| + | <math>0=\vert P'P' \vert = \vert PQ \vert </math> und damit <math>P \equiv Q</math>, was ein Widerspruch zur Annahme <math>P \not \equiv Q</math> ist. | ||
| + | =====Surjektivität von <math>\beta</math>===== | ||
| + | Wir haben zu zeigen, dass jeder Punkt <math>Q \in \varepsilon </math> bei der Bewegung <math>\beta</math> ein Urbild hat. <br /> | ||
| + | Annahme: <math>Q</math> hat kein Urbild bei <math>\beta</math>. ... | ||
Version vom 27. Mai 2018, 15:21 Uhr
Beispiele, GegenbeispieleBeispiel 1Wir gehen von der additiven Gruppe der Restklassen modulo 6 aus
Wir wählen aus
Beispiel 2Die Gruppe der BewegungenDie GruppenmitgliederUnter einer Bewegung
|
![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) .
.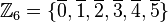

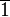

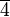
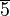
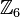 die folgende Teilmenge
die folgende Teilmenge  aus:
aus: 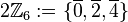
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von
ist eine Gruppe und damit eine Untergruppe von 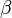 versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
versteht man eine abstandserhaltende Abbildung der Ebene auf sich: unsere Ebene.
unsere Ebene.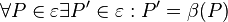

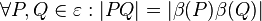
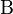 bezeichnen.
bezeichnen.
 .
.
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe
ist Gruppe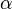 und
und  eine Bewegung ist.
eine Bewegung ist.
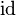 , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet:
, die jeden Punkt die Abbildung der ebene auf sich selbst abbildet: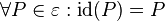
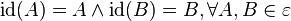 gilt natürlich auch
gilt natürlich auch 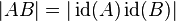 .
.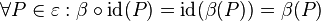 und somit
und somit 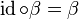 .
.
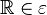 bei
bei 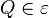 hat.
hat.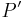 das Bild von
das Bild von  bei der Bewegung
bei der Bewegung 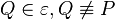 gibt, der durch
gibt, der durch 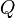 gibt. Dann gilt:
gibt. Dann gilt: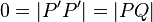 und damit
und damit 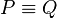 , was ein Widerspruch zur Annahme
, was ein Widerspruch zur Annahme  ist.
ist.

