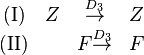Beispiele, Gegenbeispiele
Beispiel 1
Wir gehen von der additiven Gruppe der Restklassen modulo 6 aus ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) . .
Die Gruppe besteht aus den folgenden Restklassen: 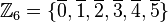
Die Gruppentafel sieht wie folgt aus:
Wir wählen aus 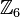 die folgende Teilmenge die folgende Teilmenge  aus: aus:
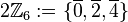
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von ist eine Gruppe und damit eine Untergruppe von ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png)
Beispiel 2
Die Gruppe der Bewegungen
Die Gruppenmitglieder
Unter einer Bewegung 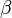 versteht man eine abstandserhaltende Abbildung der Ebene auf sich: versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
Es sei  unsere Ebene. unsere Ebene.
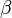 ist Relation ist Relation
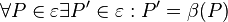
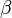 ist eindeutig und damit Abbildung ist eindeutig und damit Abbildung

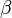 ist abstandserhaltend ist abstandserhaltend
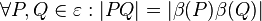
Die Menge aller Bewegungen wollen wir mit  bezeichnen. bezeichnen.
Die Verknüpfung
wir wählen als Verknüpfung auf  die NAF von Abbildungen und kennzeichnen diese mit die NAF von Abbildungen und kennzeichnen diese mit  . .
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe ist Gruppe
Abgeschlossenheit
Es seien 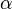 und und 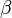 zwei Bewegungen. zwei Bewegungen.
Wir haben zu zeigen, dass  eine Bewegung ist. eine Bewegung ist.
Da die NAF zweier Abbildungen der Ebene auf sich ist tivialerweise wieder eine Abbildung der Ebene auf sich. Wir müssen nur zeigen dass  abstandserhaltend ist: abstandserhaltend ist:

Assoziativität
Die NAF von Abbildungen ist immer assoziativ.
Einselement
Wir betrachten die Abbildung 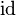 , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet: , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet:
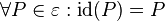
Damit ist 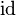 eine Abbildung der Ebene auf sich. Wegen eine Abbildung der Ebene auf sich. Wegen 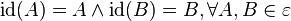 gilt natürlich auch gilt natürlich auch 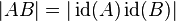 . .
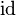 erfüllt die Eigenschaften eines Einselementes: erfüllt die Eigenschaften eines Einselementes:
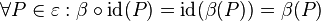 und somit und somit 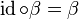 . .
inverse Elemente
Es genügt zu zeigen, dass jede Bewegung 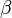 eineindeutig ist, d.h. dass jeder Punkt eineindeutig ist, d.h. dass jeder Punkt 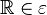 bei bei 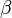 ein und nur ein Urbild ein und nur ein Urbild 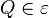 hat. hat.
Injektivität von 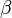
Sei 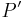 das Bild von das Bild von  bei der Bewegung bei der Bewegung 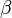 . Wir haben zu zeigen, dass es keinen Punkt . Wir haben zu zeigen, dass es keinen Punkt 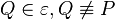 gibt, der durch gibt, der durch 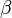 auch auf auch auf 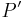 abgebildet wird. Wir nahemen, an, dass es einen solchen Punkt abgebildet wird. Wir nahemen, an, dass es einen solchen Punkt 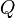 gibt. Dann gilt: gibt. Dann gilt:
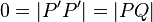 und damit und damit 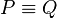 , was ein Widerspruch zur Annahme , was ein Widerspruch zur Annahme  ist. ist.
Surjektivität von 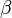
Wir haben zu zeigen, dass jeder Punkt 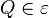 bei der Bewegung bei der Bewegung 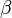 ein Urbild hat. ein Urbild hat.
Annahme: 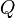 hat kein Urbild bei hat kein Urbild bei 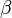 . Da jeder Punkt der Ebene . Da jeder Punkt der Ebene  durch durch 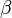 auf genau einen Punkt der Ebene auf genau einen Punkt der Ebene  abgebildet wird und der Punkt abgebildet wird und der Punkt 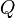 kein Urbild hat, müssen wenigstens zwei verschiedene Punkte kein Urbild hat, müssen wenigstens zwei verschiedene Punkte 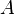 und und 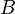 aus aus  durch durch 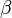 auf ein und denselben Punkt auf ein und denselben Punkt 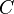 abgebildet werden: abgebildet werden:
-
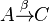
-
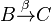
Wegen 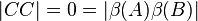 müssen müssen 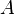 und und 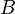 ein und derselbe Punkt, also identisch sein. Das ist ein Widerspruch zu ein und derselbe Punkt, also identisch sein. Das ist ein Widerspruch zu 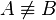 . Unsere Annahme . Unsere Annahme 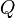 hat kein Urbild ist also zu verwerfen. hat kein Urbild ist also zu verwerfen.
Die Untergruppe der Drehungen um ein und denselben Punkt
Drehungen
- Eine Bewegung die entweder die Identität ist oder genau einen Fixpunkt
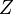 besitzt, heißt Drehung. Falls die Bewegung genau den Fixpunkt besitzt, heißt Drehung. Falls die Bewegung genau den Fixpunkt 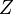 hat, sprechen wir von einer Drehung um hat, sprechen wir von einer Drehung um 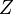 . .
Die Gruppe der Drehungen um ein und denselben Fixpunkt
Es sei 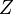 ein beliebiger aber fester Punkt der Ebene. Wir betrachten ein beliebiger aber fester Punkt der Ebene. Wir betrachten 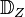 die Menge aller Drehungen um die Menge aller Drehungen um 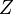 . Als Verknüpfung auf . Als Verknüpfung auf 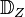 wählen wir die wählen wir die  , die NAF von Abbildungen. , die NAF von Abbildungen.
![[\mathbb{D}_Z, \circ ]](/images/math/5/5/2/552d0d83fed54a94d1775beb5f9391f9.png) ist eine Gruppe: ist eine Gruppe:
Abgeschlossenheit
Es seien 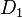 und und 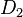 zwei Drehungen um zwei Drehungen um 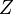 . Wir haben bererits geszeigt, dass die NAF zweier Bewegungen eine Bewegung ist. Da . Wir haben bererits geszeigt, dass die NAF zweier Bewegungen eine Bewegung ist. Da 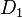 und und 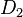 zwei Bewegungen sind, ist zwei Bewegungen sind, ist 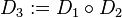 ebenfalls eine Bewegung. Weil ebenfalls eine Bewegung. Weil 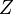 ein Fixpunkt sowohl von ein Fixpunkt sowohl von 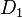 als auch von als auch von 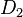 ist, muss ist, muss 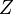 auch ein Fixpunkt von auch ein Fixpunkt von  sein. Es können jetzt genau zwei Fälle auftreten: sein. Es können jetzt genau zwei Fälle auftreten:
Fall 1
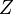 ist der einzige Fixpunkt von ist der einzige Fixpunkt von  . In diesem Fall ist . In diesem Fall ist  eine Drehung mit dem Fixpunkt eine Drehung mit dem Fixpunkt 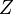 . .
Fall 2
 hat neben hat neben 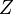 einen weiteren Fixpunkt einen weiteren Fixpunkt 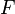 . .
Das bedeutet:
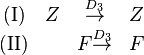
| ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) .
.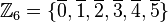

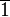

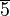
 die folgende Teilmenge
die folgende Teilmenge  aus:
aus: 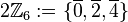
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von
ist eine Gruppe und damit eine Untergruppe von  versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
versteht man eine abstandserhaltende Abbildung der Ebene auf sich: unsere Ebene.
unsere Ebene.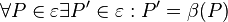

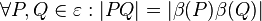
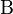 bezeichnen.
bezeichnen.
 .
.
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe
ist Gruppe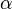 und
und  eine Bewegung ist.
eine Bewegung ist.
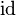 , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet:
, die jeden Punkt die Abbildung der ebene auf sich selbst abbildet: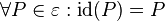
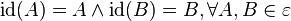 gilt natürlich auch
gilt natürlich auch 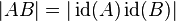 .
.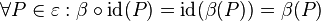 und somit
und somit 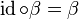 .
.
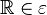 bei
bei 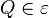 hat.
hat.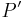 das Bild von
das Bild von  bei der Bewegung
bei der Bewegung 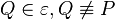 gibt, der durch
gibt, der durch 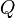 gibt. Dann gilt:
gibt. Dann gilt: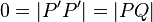 und damit
und damit 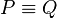 , was ein Widerspruch zur Annahme
, was ein Widerspruch zur Annahme  ist.
ist.
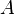 und
und 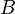 aus
aus 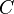 abgebildet werden:
abgebildet werden: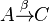
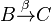
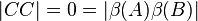 müssen
müssen 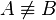 . Unsere Annahme
. Unsere Annahme 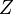 besitzt, heißt Drehung. Falls die Bewegung genau den Fixpunkt
besitzt, heißt Drehung. Falls die Bewegung genau den Fixpunkt 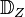 die Menge aller Drehungen um
die Menge aller Drehungen um ![[\mathbb{D}_Z, \circ ]](/images/math/5/5/2/552d0d83fed54a94d1775beb5f9391f9.png) ist eine Gruppe:
ist eine Gruppe:
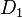 und
und 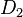 zwei Drehungen um
zwei Drehungen um 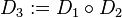 ebenfalls eine Bewegung. Weil
ebenfalls eine Bewegung. Weil  sein. Es können jetzt genau zwei Fälle auftreten:
sein. Es können jetzt genau zwei Fälle auftreten:
 .
.