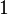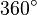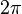Serie 5: Parameterdarstellungen I SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.1) |
||
| Zeile 5: | Zeile 5: | ||
=Aufgabe 5.1= | =Aufgabe 5.1= | ||
| − | Wir legen unseren Betrachtungen ein kartesisches Koordinatensystem mit dem Koordinatenursprung <math>O</math> zugrunde. Es seien <math>k</math> ein Einheitskreis in Mittelpunktslage | + | Wir legen unseren Betrachtungen ein kartesisches Koordinatensystem mit dem Koordinatenursprung <math>O</math> zugrunde. Es seien <math>k</math> ein Einheitskreis in Mittelpunktslage und <math>A</math> der Schnittpunkt von <math>k</math> mit der positiven <math>x-</math>Achse. Der Punkt <math>P</math> möge sich auf dem Kreis bewegen und zunächst mit $A$ zusammenfallen. Den Winkel <math>\angle AOP</math> bezeichnen wir mit <math>\varphi</math>. Wir verstehen <math>\varphi</math> als gerichteten Winkel, d.h. bewegt sich <math>P</math> hinreichend lange mit mathematisch negativen Drehsinn (mit dem Uhrzeigersinn) auf <math>k</math> wird <math>\varphi</math> negativ.<br /> |
| − | [https://ggbm.at/zschkpuv geogebraApp] | + | |
| + | [https://ggbm.at/zschkpuv geogebraApp]<br /> | ||
| + | Ergänzen Sie die folgende Tabelle:<br /> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Umdrehungen von <math>P</math> !! <math>\varphi</math> in Gradmaß !! <math>\varphi</math> in Bogenmaß | ||
| + | |- | ||
| + | | <math>1</math> || <math>360^\circ</math> || <math>2\pi</math> | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |- | ||
| + | | Beispiel || Beispiel || Beispiel | ||
| + | |} | ||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Version vom 1. Juli 2018, 15:34 Uhr
Aufgabe 5.1Wir legen unseren Betrachtungen ein kartesisches Koordinatensystem mit dem Koordinatenursprung geogebraApp
|
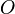 zugrunde. Es seien
zugrunde. Es seien  ein Einheitskreis in Mittelpunktslage und
ein Einheitskreis in Mittelpunktslage und  der Schnittpunkt von
der Schnittpunkt von 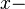 Achse. Der Punkt
Achse. Der Punkt  möge sich auf dem Kreis bewegen und zunächst mit $A$ zusammenfallen. Den Winkel
möge sich auf dem Kreis bewegen und zunächst mit $A$ zusammenfallen. Den Winkel 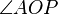 bezeichnen wir mit
bezeichnen wir mit  . Wir verstehen
. Wir verstehen