Aufgabe 5.1
Wir legen unseren Betrachtungen ein kartesisches Koordinatensystem mit dem Koordinatenursprung 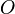 zugrunde. Es seien zugrunde. Es seien  ein Einheitskreis in Mittelpunktslage und ein Einheitskreis in Mittelpunktslage und  der Schnittpunkt von der Schnittpunkt von  mit der positiven mit der positiven 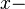 Achse. Der Punkt Achse. Der Punkt  möge sich auf dem Kreis bewegen und zunächst mit $A$ zusammenfallen. Den Winkel möge sich auf dem Kreis bewegen und zunächst mit $A$ zusammenfallen. Den Winkel 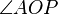 bezeichnen wir mit bezeichnen wir mit  . Wir verstehen . Wir verstehen  als gerichteten Winkel, d.h. bewegt sich als gerichteten Winkel, d.h. bewegt sich  hinreichend lange mit mathematisch negativen Drehsinn (mit dem Uhrzeigersinn) auf hinreichend lange mit mathematisch negativen Drehsinn (mit dem Uhrzeigersinn) auf  wird wird  negativ. negativ.
geogebraApp
Ergänzen Sie die folgende Tabelle:
Umdrehungen von  |
 in Gradmaß in Gradmaß |
 in Bogenmaß in Bogenmaß
|
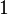 |
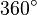 |
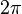
|
 |
 |

|
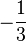 |
 |

|
 |
 |
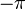
|
 |
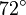 |

|
 |
 |

|
 |
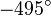 |

|
 |
 |
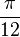
|
 |
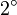 |

|
 |
 |
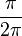
|
Aufgabe 5.2
Eine Punktmasse  bewegt sich gleichförmig auf einem Einheitskreis bewegt sich gleichförmig auf einem Einheitskreis  in Mittelpunktslage mit einer Frequenz von in Mittelpunktslage mit einer Frequenz von 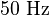 , d.h. sie vollführt 50 Umdrehungen pro Sekunde. ( , d.h. sie vollführt 50 Umdrehungen pro Sekunde. (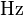 ist die Abkürzung für die Einheit ist die Abkürzung für die Einheit 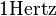 . Sie wurde zu Ehren des deutschen Physikers Heinrich Hertz eingeführt. Es gilt . Sie wurde zu Ehren des deutschen Physikers Heinrich Hertz eingeführt. Es gilt 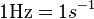 .) Welchen Weg hat .) Welchen Weg hat  nach nach
-
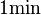 , ,
-
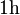 , ,
-
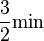
-
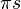
zurück gelegt?
Aufgabe 5.3
Eine Punktmasse  bewegt sich gleichförmig auf einem Einheitskreis bewegt sich gleichförmig auf einem Einheitskreis  in Mittelpunktslage mit folgenden Frequenzen in Mittelpunktslage mit folgenden Frequenzen  : :
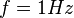
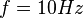
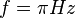
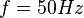
Die sogenannte Kreisfrequenz (Winkelfrequenz) 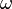 berechnet sich zu berechnet sich zu 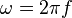 . Berechnen Sie die zugehörigen Kreisfrequenzen und interpretieren Sie diese sowohl physikalisch als auch geometrisch. . Berechnen Sie die zugehörigen Kreisfrequenzen und interpretieren Sie diese sowohl physikalisch als auch geometrisch.
| 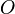 zugrunde. Es seien
zugrunde. Es seien  ein Einheitskreis in Mittelpunktslage und
ein Einheitskreis in Mittelpunktslage und  der Schnittpunkt von
der Schnittpunkt von 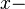 Achse. Der Punkt
Achse. Der Punkt  möge sich auf dem Kreis bewegen und zunächst mit $A$ zusammenfallen. Den Winkel
möge sich auf dem Kreis bewegen und zunächst mit $A$ zusammenfallen. Den Winkel 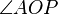 bezeichnen wir mit
bezeichnen wir mit  . Wir verstehen
. Wir verstehen 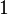
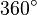
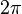


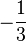
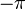
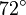

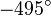
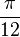
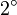
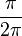
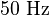 , d.h. sie vollführt 50 Umdrehungen pro Sekunde. (
, d.h. sie vollführt 50 Umdrehungen pro Sekunde. (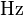 ist die Abkürzung für die Einheit
ist die Abkürzung für die Einheit 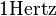 . Sie wurde zu Ehren des deutschen Physikers Heinrich Hertz eingeführt. Es gilt
. Sie wurde zu Ehren des deutschen Physikers Heinrich Hertz eingeführt. Es gilt 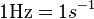 .) Welchen Weg hat
.) Welchen Weg hat 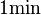 ,
,
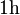 ,
,
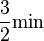
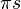
 :
:
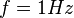
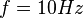
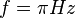
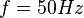
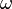 berechnet sich zu
berechnet sich zu 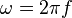 . Berechnen Sie die zugehörigen Kreisfrequenzen und interpretieren Sie diese sowohl physikalisch als auch geometrisch.
. Berechnen Sie die zugehörigen Kreisfrequenzen und interpretieren Sie diese sowohl physikalisch als auch geometrisch.

