Lösung von Zusatzaufgabe 6.1 P (WS 18 19): Unterschied zwischen den Versionen
CIG UA (Diskussion | Beiträge) |
|||
| Zeile 17: | Zeile 17: | ||
3. b hat zwei Parallelen, die durch P verlaufen - '''1.'''<br /> | 3. b hat zwei Parallelen, die durch P verlaufen - '''1.'''<br /> | ||
4. b hat genau eine Parallele durch P - '''Parallelenaxiom'''<br /> | 4. b hat genau eine Parallele durch P - '''Parallelenaxiom'''<br /> | ||
| + | an dieser 4. Stelle können Sie auch gleich "Widerspruch zum Parallelenaxiom" anführen--[[Benutzer:Schnirch|Schnirch]] ([[Benutzer Diskussion:Schnirch|Diskussion]]) 13:49, 29. Nov. 2018 (CET) | ||
5. Widerspruch, Annahme ist zu verwerfen - '''3., 4.''' | 5. Widerspruch, Annahme ist zu verwerfen - '''3., 4.''' | ||
Aktuelle Version vom 29. November 2018, 13:49 Uhr
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: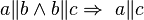 
.
b) Welche Eigenschaft der Relation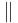 
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
a)
Vor: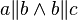 
Ann: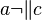 
1. a und c haben einen (gemeinsamen) Schnittpunkt P - Ann
2. b hat keinen gemeinsamen Punkt mit a und c (P liegt nicht auf b) - Vor
3. b hat zwei Parallelen, die durch P verlaufen - 1.
4. b hat genau eine Parallele durch P - Parallelenaxiom
an dieser 4. Stelle können Sie auch gleich "Widerspruch zum Parallelenaxiom" anführen--Schnirch (Diskussion) 13:49, 29. Nov. 2018 (CET)
5. Widerspruch, Annahme ist zu verwerfen - 3., 4.
b)
Die Transitivität
--CIG UA (Diskussion) 13:54, 23. Nov. 2018 (CET)
