Serie 1 Geradengleichungen in der Ebene: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3) |
||
| Zeile 14: | Zeile 14: | ||
=Aufgabe 3= | =Aufgabe 3= | ||
| − | Eine Gerade <math>g</math> habe ein Anstiegsdreieck, dessen zur <math>y-</math> Achse parallele Kathete die Länge <math>\Delta y</math> hat. Die andere Kathete möge die Länge <math>\Delta x</math> haben. Geben sie fünf Vektoren <math>\overrightarrow{n_1}, \overrightarrow{n_2}, \overrightarrow{n_3}, \overrightarrow{n_4}, \overrightarrow{n_5}</math> an, die bezüglich <math>g</math> Normalenvektoren sind. | + | Eine Gerade <math>g</math> habe ein Anstiegsdreieck, dessen zur <math>y-</math> Achse parallele Kathete die Länge <math>\Delta y</math> hat. Die andere Kathete möge die Länge <math>\Delta x</math> haben. Geben sie fünf Vektoren <math>\overrightarrow{n_1}, \overrightarrow{n_2}, \overrightarrow{n_3}, \overrightarrow{n_4}, \overrightarrow{n_5}</math> an, die bezüglich <math>g</math> Normalenvektoren sind. Einer dieser Vektoren möge die Länge <math>1</math> haben, d.h. ein Normaleneinheitsvektor sein. |
| + | =Aufgabe 4= | ||
| + | Zeichnen Sie auf ein Blatt Papier ein kartesisches Koordinatensystem. | ||
| + | # Zeichen Sie bezüglich dieses Koordinatensystems die Gerade <math>g</math> ein, die durch die Gleichung <math>y=\frac{3}{5}x</math> beschrieben wird. | ||
| + | # Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade <math>h</math> ein, die durch die Gleichung <math>\frac{3}{5}x-\frac{4}{5}=0</math> beschrieben wird. | ||
| + | # Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade <math>i</math> ein, die durch die Gleichung <math>-3x+4y=0</math> beschrieben wird. | ||
| + | # Interpretieren Sie die Gleichungen für <math>h</math> und <math>i</math> als <math>ax+by=0</math>. Zeichnen Sie für beide Geraden jeweils die Vektoren <math>\begin{pmatrix} a \\ b \end{pmatrix}</math> ein. | ||
| + | # Zeichnen Sie den Punkt <math>P\left(10, \frac{10}{8} \right)</math> ein. Messen Sie den Abstand von <math>P</math> zu <math>g</math>. | ||
| + | # Berechnen Sie <math>\frac{3}{5}10-\frac{4}{5}\frac{10}{8}=d</math>. Was stellen Sie fest? | ||
Version vom 2. Mai 2019, 15:43 Uhr
Inhaltsverzeichnis |
Aufgabe 1
Gegeben seien die Punkte 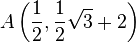 und
und 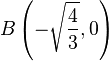 .
.
Beschreiben Sie die Gerade  jeweils durch eine Gleichung der Form
jeweils durch eine Gleichung der Form
.
Aufgabe 2
Die Gerade  möge die
möge die 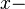 Achse unter einem Winkel von
Achse unter einem Winkel von 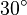 im Punkt
im Punkt 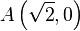 schneiden.
schneiden.
- Zeichnen Sie ein kartesisches Koordinatensystem auf ein Blatt Papier. Konstruieren Sie nur mit Zirkel und Lineal eine grafische Darstellung der Geraden
 bezüglich Ihres Koordinatensystems.
bezüglich Ihres Koordinatensystems.
- Geben Sie eine Gleichung der Form
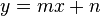 zur Beschreibung von
zur Beschreibung von  an.
an.
- Geben Sie eine Gleichung der Form
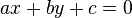 zur Beschreibung von
zur Beschreibung von  an.
an.
- Geben Sie eine Gleichung der Form
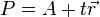 zur Beschreibung von
zur Beschreibung von  an.
an.
Aufgabe 3
Eine Gerade  habe ein Anstiegsdreieck, dessen zur
habe ein Anstiegsdreieck, dessen zur 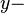 Achse parallele Kathete die Länge
Achse parallele Kathete die Länge 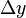 hat. Die andere Kathete möge die Länge
hat. Die andere Kathete möge die Länge 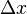 haben. Geben sie fünf Vektoren
haben. Geben sie fünf Vektoren 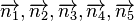 an, die bezüglich
an, die bezüglich  Normalenvektoren sind. Einer dieser Vektoren möge die Länge
Normalenvektoren sind. Einer dieser Vektoren möge die Länge 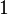 haben, d.h. ein Normaleneinheitsvektor sein.
haben, d.h. ein Normaleneinheitsvektor sein.
Aufgabe 4
Zeichnen Sie auf ein Blatt Papier ein kartesisches Koordinatensystem.
- Zeichen Sie bezüglich dieses Koordinatensystems die Gerade
 ein, die durch die Gleichung
ein, die durch die Gleichung 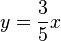 beschrieben wird.
beschrieben wird.
- Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade
 ein, die durch die Gleichung
ein, die durch die Gleichung 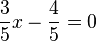 beschrieben wird.
beschrieben wird.
- Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade
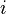 ein, die durch die Gleichung
ein, die durch die Gleichung 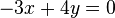 beschrieben wird.
beschrieben wird.
- Interpretieren Sie die Gleichungen für
 und
und 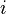 als
als 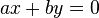 . Zeichnen Sie für beide Geraden jeweils die Vektoren
. Zeichnen Sie für beide Geraden jeweils die Vektoren 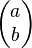 ein.
ein.
- Zeichnen Sie den Punkt
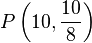 ein. Messen Sie den Abstand von
ein. Messen Sie den Abstand von  zu
zu  .
.
- Berechnen Sie
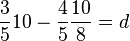 . Was stellen Sie fest?
. Was stellen Sie fest?

