Der Umkreis und die Mittelsenkrechten eines Dreiecks: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition XIII.1 : (Umkreis eines Dreiecks))
Zeile 10: Zeile 10:
 
===== Satz XIII.1 (Schnittpunkt der Mittelsenkrechten eines Dreiecks) =====
 
===== Satz XIII.1 (Schnittpunkt der Mittelsenkrechten eines Dreiecks) =====
 
::Die Mittelsenkrechten eines Dreiecks schneiden einander in genau einem Punkt.
 
::Die Mittelsenkrechten eines Dreiecks schneiden einander in genau einem Punkt.
 +
 +
'''Beweis: Existenz und Eindeutigkeit eines Schnittpunktes der Mittelsenkrechten eines Dreiecks'''
 +
<br />Man muss also beweisen, dass es...
 +
::(1) einen Schnittpunkt aller drei Mittelsenkrechten gibt
 +
::(2) GENAU einen Schnittpunkt gibt
 +
 +
Dies findet jedoch nicht in diesen zwei Schritten wie üblich statt, da andere Grundvoraussetzungen geklärt werden müssen.
 +
Zur besseren Veranschaulichung sei die Vorgehensweise:
 +
::(a) Die drei Mittelsenkrechten schneiden sich: vielleicht in einem, vielleicht in drei verschiedenen Punkten (Grundvoraussetzung)
 +
::(b) Es existiert ein Schnittpunkt von zwei Mittelsenkrechten
 +
::(c) Es existiert ein Schnittpunkt der beiden Mittelsenkrechten aus (b) und der dritten Mittelsenkrechten
 +
 +
Etwas formloser nun ohne Voraussetzung und Behauptung:
 +
::(a) Die drei Mittelsenkrechten schneiden sich: vielleicht in einem, vielleicht in drei verschiedenen Punkten (Grundvoraussetzung)
 +
:::(I) Die drei Eckpunkte des Dreiecks sind nicht kollinear (Konstruktion eines Dreiecks)
 +
:::(II) Daraus resultieren drei Geraden <math>\ AB, BC, AC</math>, die paarweise nicht identisch sind (I)
 +
:::(III) "Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam."  (Satz I.1)
 +
:::(III)a Keine Seite eines Dreiecks kann parallel zu einer zweiten Seite des Dreiecks sein.
 +
:::(IV) Die Senkrechten auf zwei nicht-identischen, nicht-parallen Geraden schneiden sich (da nur die Senkrechten von parallelen Geraden schnittpunktfrei sind --> die Senkrechte zur Senkrechten einer Gerade ist die Parallele zur Geraden)
 +
 +
 +
::(b) Es existiert ein Schnittpunkt von zwei Mittelsenkrechten
 +
:::(I) Alle Punkte <math>P_\mathrm{mb} \in m_b</math> haben selben Abstand zu <math>\ A</math> und <math>\ C</math> (Mittelsenkrechtenkriterium)
 +
:::(II) Alle Punkte <math>P_\mathrm{ma} \in m_a</math> haben selben Abstand zu <math>\ B</math> und <math>\ C</math> (Mittelsenkrechtenkriterium)
 +
:::(III) <math>\ m_b</math> und <math>\ m_a</math> schneiden sich in <math>\ S</math> (Existenz des Schnittpunktes nach Teil (a) bewiesen)
 +
:::(IV) Da <math>S \in m_b \wedge S \in m_a</math> gilt <math>|AS| = |CS|</math> und <math>|BS| = |CS|</math>
 +
 +
::(c) Es existiert ein Schnittpunkt der beiden Mittelsenkrechten aus (b) und der dritten Mittelsenkrechten
 +
:::(I) Es gilt <math>|AS| = |CS|</math> und <math>|BS| = |CS|</math> nach (b)(IV)
 +
:::(II) Es gilt auch <math>|AS| = |BS|</math> nach (I) (Transitivität, Umformung)
 +
:::(III) Es gilt somit auch: <math>S \in m_c</math> (Mittelsenkrechtenkriterium)
 +
 +
Es existiert genau ein Schnittpunkt!
 +
 +
Muss man die Eindeutigkeit jetzt noch beweisen? Und wenn nicht: warum nicht? --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 15:00, 22. Jul. 2010 (UTC)

Version vom 22. Juli 2010, 16:00 Uhr

Inhaltsverzeichnis

Umkreis eines Dreiecks

Definition XIII.1 : (Mittelsenkrechten eies Dreiecks)
Unter den Mittelsenkrechten eines Dreiecks versteht man die Mittelsenkrechten der Seiten dieses Dreiecks.
Definition XIII.2 : (Umkreis eines Dreiecks)
Wenn ein Kreis \ k durch die Eckpunkte \ A , B, C des Dreiecks \overline{ABC} geht, dann ist \ k der Umkreis des Dreiecks \overline{ABC}.

Satz XIII.1 (Schnittpunkt der Mittelsenkrechten eines Dreiecks)
Die Mittelsenkrechten eines Dreiecks schneiden einander in genau einem Punkt.

Beweis: Existenz und Eindeutigkeit eines Schnittpunktes der Mittelsenkrechten eines Dreiecks
Man muss also beweisen, dass es...

(1) einen Schnittpunkt aller drei Mittelsenkrechten gibt
(2) GENAU einen Schnittpunkt gibt

Dies findet jedoch nicht in diesen zwei Schritten wie üblich statt, da andere Grundvoraussetzungen geklärt werden müssen. Zur besseren Veranschaulichung sei die Vorgehensweise:

(a) Die drei Mittelsenkrechten schneiden sich: vielleicht in einem, vielleicht in drei verschiedenen Punkten (Grundvoraussetzung)
(b) Es existiert ein Schnittpunkt von zwei Mittelsenkrechten
(c) Es existiert ein Schnittpunkt der beiden Mittelsenkrechten aus (b) und der dritten Mittelsenkrechten

Etwas formloser nun ohne Voraussetzung und Behauptung:

(a) Die drei Mittelsenkrechten schneiden sich: vielleicht in einem, vielleicht in drei verschiedenen Punkten (Grundvoraussetzung)
(I) Die drei Eckpunkte des Dreiecks sind nicht kollinear (Konstruktion eines Dreiecks)
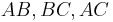(II) Daraus resultieren drei Geraden \ AB, BC, AC, die paarweise nicht identisch sind (I)
(III) "Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam." (Satz I.1)
(III)a Keine Seite eines Dreiecks kann parallel zu einer zweiten Seite des Dreiecks sein.
(IV) Die Senkrechten auf zwei nicht-identischen, nicht-parallen Geraden schneiden sich (da nur die Senkrechten von parallelen Geraden schnittpunktfrei sind --> die Senkrechte zur Senkrechten einer Gerade ist die Parallele zur Geraden)


(b) Es existiert ein Schnittpunkt von zwei Mittelsenkrechten
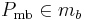(I) Alle Punkte P_\mathrm{mb} \in m_b haben selben Abstand zu \ A und \ C (Mittelsenkrechtenkriterium)
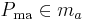(II) Alle Punkte P_\mathrm{ma} \in m_a haben selben Abstand zu \ B und \ C (Mittelsenkrechtenkriterium)
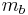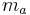(III) \ m_b und \ m_a schneiden sich in \ S (Existenz des Schnittpunktes nach Teil (a) bewiesen)
(IV) Da 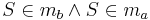S \in m_b \wedge S \in m_a gilt |AS| = |CS| und |BS| = |CS|
(c) Es existiert ein Schnittpunkt der beiden Mittelsenkrechten aus (b) und der dritten Mittelsenkrechten
(I) Es gilt |AS| = |CS| und |BS| = |CS| nach (b)(IV)
(II) Es gilt auch 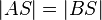|AS| = |BS| nach (I) (Transitivität, Umformung)
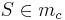(III) Es gilt somit auch: S \in m_c (Mittelsenkrechtenkriterium)

Es existiert genau ein Schnittpunkt!

Muss man die Eindeutigkeit jetzt noch beweisen? Und wenn nicht: warum nicht? --Heinzvaneugen 15:00, 22. Jul. 2010 (UTC)

Von „http://geometrie.zum.de/index.php?title=Der_Umkreis_und_die_Mittelsenkrechten_eines_Dreiecks&oldid=3620“