Diskussion:Lösung von Aufgabe 13.1: Unterschied zwischen den Versionen

Version vom 22. Juli 2010, 18:38 Uhr

zu Heinzvaneugen von --Löwenzahn 15:19, 21. Jul. 2010 (UTC):

Könnte man Fall 2 nicht direkt widerlegen, da wenn a < b dann folgt 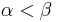$\alpha < \beta$ (das war doch bereits gezeigt?!), was ein Widerspruch zur VSS wäre?
zu Schritt zwei... man darf (meines Wissens nach) keine Umkehrung eines Axioms verwenden, das ist nur bei Sätzen und Definitionen möglich, aber nicht bei Axiomen. Die Argumentation nach Axiom von Pasch geht auch nicht, da dieses aussagt: "wird eine Seite eines Dreiecks geschnitten, so wird auch eine weitere geschnitten", da aber der Strahl in einem Eckpunkt anfängt, darf das Axiom nicht verwendet werden. Ich denke durch die "Geschichten im Inneren" würde die Argumentation passen. Durch das Winkelmaßaxiom hast du ja den WInkel $\beta$ abgetragen, der nach VSS kleiner als $\alpha$ ist. Und dann hatten wir ja die Sätze: "Ist ein Strahl im Inneren eines Winkels so schneiden er die Strecke etc."
Ich verstehe irgendwie den Schritt IV nicht. Wie begründest du dass die Seite kleiner wird, wenn der Winkel kleiner wird??? Du beziehst dich bei der Beweisführung insgesamt auch nicht auf deine ANN, oder?

Re: --Heinzvaneugen 17:56, 21. Jul. 2010 (UTC)

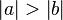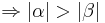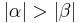Bin mir da nicht so sicher. Haben wir nicht die Umkehrung bewiesen? Also dass gilt: Wenn $\left| a \right| >\left| b \right|$ (VSS) $\Rightarrow \left| \alpha \right| > \left| \beta \right|$ (Beh.) Jetzt haben wir allerdings die Voraussetzung: $\ |\alpha| > |\beta|$ .
Das war der eine Knackpunkt des Beweises, bislang wurde auch am häufigsten zur Begründung "Geschichten aus dem Inneren" untestützt.
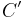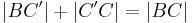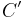Das war der zweite Knackpunkt, ob es reicht zu zeigen, dass (da $\ C'$ zwischen $\ B$ und $\ C$ liegt) gilt $\ |BC'| + |C'C| = |BC|$ . Und da $\ C$ und $\ C'$ nicht identisch sind, ist 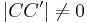$\ |CC'| \ne 0$ und deshalb $\ |BC'| < |BC|$ .

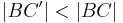Re: --Löwenzahn 17:38, 22. Jul. 2010 (UTC)

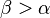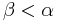Wir haben doch bewiesen, dass der Satz "größere Seite --> größerer Winkel" stimmt. Und da du ja in Schritt 2 die ANN hast, dass a < b , bzw rumgedreht b > a kannst du ja nach dem Satz (größere Seite --> größerer Winkel) davon ausgehen, dass $\beta > \alpha$ ist, was ein Widerspruch zur VSS ist, dass $\beta < \alpha$ . Somit wäre ja Fall 2 auch widerlegt, und die ANN ist zu verwerfen, die Beh stimmt. (dann bräuchte man die restlichen Schritte doch gar nicht)
zu 2 und 3: habe grad keine Idee, wie man das weiter führen/ändern könnte. Vielleicht sagt Herr Gieding morgen was in der Übung.

@@ Zeile 10: / Zeile 10: @@
 # Das war der eine Knackpunkt des Beweises, bislang wurde auch am häufigsten zur Begründung "Geschichten aus dem Inneren" untestützt.
 # Das war der zweite Knackpunkt, ob es reicht zu zeigen, dass (da <math>\ C'</math> zwischen <math>\ B</math> und <math>\ C</math> liegt) gilt <math>\ |BC'| + |C'C| = |BC|</math>. Und da <math>\ C</math> und <math>\ C'</math> nicht identisch sind, ist <math>\ |CC'| \ne 0</math> und deshalb <math>\ |BC'| < |BC|</math>.
+Re: --[[Benutzer:Löwenzahn|Löwenzahn]] 17:38, 22. Jul. 2010 (UTC)
+# Wir haben doch bewiesen, dass der Satz "größere Seite --> größerer Winkel" stimmt. Und da du ja in Schritt 2 die ANN hast, dass a < b , bzw rumgedreht b > a kannst du ja nach dem Satz (größere Seite --> größerer Winkel) davon ausgehen, dass <math> \beta > \alpha </math> ist, was ein Widerspruch zur VSS ist, dass <math> \beta < \alpha </math>. Somit wäre ja Fall 2 auch widerlegt, und die ANN ist zu verwerfen, die Beh stimmt. (dann bräuchte man die restlichen Schritte doch gar nicht)
+# zu 2 und 3: habe grad keine Idee, wie man das weiter führen/ändern könnte. Vielleicht sagt Herr Gieding morgen was in der Übung.