Lösung von Aufgabe 13.1
Aus Geometrie-Wiki
Beweisen Sie den Satz: Wenn ein Innenwinkel eines Dreiecks größer ist als ein anderer Innenwinkel dieses Dreiecks ist, dann ist die Seite, die ihm gegenüber liegt, größer als die Seite, die dem kleineren Winkel gegenüber liegt.
Satz IX.3
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 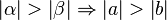
- Es sei
Beweis von Satz IX.3
Fallunterscheidung:
Voraussetzung: 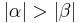
Behauptung: 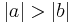
Annahme: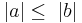
Aus "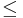 " lassen sich zwei Fälle ableiten:
" lassen sich zwei Fälle ableiten:
- )
 , dann gilt allerdings
, dann gilt allerdings 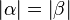 , da es sich um ein gleichschenkliges Dreieck handelt, bei dem bekanntlich die Basiswinkel kongruent sind --> Widerspruch zur VSS!
, da es sich um ein gleichschenkliges Dreieck handelt, bei dem bekanntlich die Basiswinkel kongruent sind --> Widerspruch zur VSS!
- )
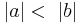 , das ist allerdings der Fall, wenn
, das ist allerdings der Fall, wenn 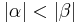 (zu beweisen, analog zu Satz IX.2)
(zu beweisen, analog zu Satz IX.2)
Beweis (Fall 2):
Voraussetzung: 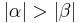
Behauptung: 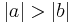
Annahme: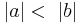
Annahme: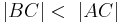
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Am Scheitelpunkt  wird der Winkel wird der Winkel  derart abgetragen, dass derart abgetragen, dass 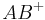 den einen Strahl des Winkels darstellt und der andere Strahl den einen Strahl des Winkels darstellt und der andere Strahl 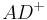 in der Halbebene in der Halbebene 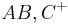 liegt liegt
|
Winkelkonstruktionsaxiom |
| (II) | Der Strahl 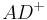 schneidet die Seite schneidet die Seite  in einem Punkt in einem Punkt 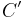 . . 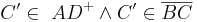
|
Axiom von Pasch (geht das? oder reicht der Verweis auf die "Geschichten aus dem Inneren") oder Umkehrung Axiom IV.3: (Winkeladditionsaxiom), da der Winkel 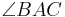 sich aus sich aus 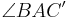 und und 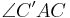 zusammensetzt. zusammensetzt.
|
| (III) | Die Länge der Strecke 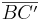 ist kleiner als die Länge der Strecke ist kleiner als die Länge der Strecke 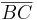
|
Es gilt 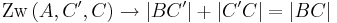
|
| (IV) | Wenn Voraussetzung: 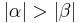 ist die Stercke ist die Stercke 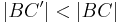 . .
|
(III) 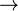 Wenn Wenn  kleiner wird, verkleinert sich auch die gegenüberliegende Seite kleiner wird, verkleinert sich auch die gegenüberliegende Seite
|
Annahme muss verworfen werden.
Kommentar: Noch nie war ich mir bei einer Beweisführung so unsichre. Please comment! Geht das so? Darf ich aus (IV) das schließen? --Heinzvaneugen 14:41, 21. Jul. 2010 (UTC)

