Diskussion:Elementargeometrie: Unterschied zwischen den Versionen
(→Kontrollfragen) |
|||
| Zeile 12: | Zeile 12: | ||
Definiert man "Inneres eines Vierecks/Dreiecks" über die Schnittmenge der vier bzw. drei Halbebenen (analog zum Inneren eines Winkels)? | Definiert man "Inneres eines Vierecks/Dreiecks" über die Schnittmenge der vier bzw. drei Halbebenen (analog zum Inneren eines Winkels)? | ||
| + | |||
| + | |||
| + | Ich würde es so machen... | ||
| + | |||
| + | <ggb_applet width="884" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAMWOXj0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VhNc+M2DD13fwVH98j6sGx5xs5O4lwys+0evLuH3igJkdlIpEpSiZ1fX5CUbMneacfd7UwdXyQCEAS8BxC0lh93dUVeQCom+MoL/cAjwHNRMF6uvFY/3aTex9sPyxJECZmk5EnImuqVF/uRZ+Qtu/3wy1JtxSuhlTX5xuB15WnZgkdUI4EWagugnfiJVgrltN2xilG5/5z9AblWR4Xz8cibVvdO8rr4xFS/nNj3NRXTD+yFFSBJJfKVN0swcrz7BlKznFYrbxo4SbTyohMlimKj3QrJ3gTXxvzo/AklhCj2BghIZGTLic1zCW1esYJRbpKxcaARIa+s0FsMIUrRJbByi7EmYeC85ULIYrNXGmqy+x2kwHDCxOC8d6vYrRTGhS9MAqsarqwbeNmA1siKInQHR8BKyYrR4lHdi+ooagTjek0b3UpLadyJNnpvXoDvkibgO15W0MkihHwL+XMmdhsHQuxcf9k39hEbUFauRSUkkQbeBA26a+au1sZEerAKrE1gLTofxulBHy4ia2Gvmbtaq4pxF1qXedhn3UNMd0wRIzAwYiUekq9oBkitR1rO9Kd+gSXw3KUaugd+a+sMW2BYBAef4c/yuZyclM/yGSSHyhUJR25b0SryYorRvcsGUkDOalw6RQcJNXR9xQCctIBSQh+46yAHmNWOCvFEvJz0QZgYFMaaa9wJMB9tcjGdqrFLzF1BtZGYNqigBuwRbevBltMBlzvvsB8I29t9F3f6I8Ko/m5t2CqiVbOlKOnLv6J77PRhOtbfr6IYJ0k5gmUzwIZrjANDRwPgmNRdBZMGHdp+GCBtAVJkt/JuIn82wy7Eu9BP02D4Qy9vbqO0D7lmMtuADSPumHYI/QNW9+8Bq6mfRCOAEgtc6IfT/wq39XvADWsscTU29Rc/D5uHd4FN4M+D0+rZG2+LHyqqXNQ15QXhtMYwNlAauQWMmQMHoYHZwAgNTW86kFrdK6jz1vk4o0F13nqgqTeeXXqLI4KDUnbA6uEo/RG2gn/P1QDv2A++18RzP0zP4U786WzY8+HpmP6bVOFP7myUG5asxpNczvQB7cqUxSPXODrBjqLzifgM0JijyGf+RVKuzInU2Qwm7UWU3zvK12eUZ5dRnl0X5fPZiPLIDby5H6SW5giPpbPZoN+Sa+d57Xh+OOM5v4zn/Ip4jv3FmOZpN57TZDH69TtpFA/tr57zB8f53RnnxWWcF1fEeeSn49087s+yi5mlOfbTcNjZwfyd0Hw+teEymuGKaMZT0phmw6MhOvGjkcKN7Rvcz6ezdCj+H5M+Gf4dtV9gui9Qt38BUEsHCAdpSpHbAwAAsxIAAFBLAQIUABQACAAIAMWOXj0HaUqR2wMAALMSAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAFQQAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | |||
| + | |||
| + | <ggb_applet width="884" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAGKPXj0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VhLc9s4DD5vfwVH98h62I4zY6eTOpfMdLcHtz30RkmIzEYiVZJK7Pz6BQnJluO2O97NYR1fZIIQCHwfHrTn7zd1xR5BG6HkIojDKGAgc1UIWS6C1t5fzIL31+/mJagSMs3ZvdI1t4sgDZPAyVtx/e6PuVmrJ8Yrr/JVwNMisLqFgJlGAy/MGsCS+J5XBuW83YhKcL39lH2H3Jr9Btm4k01reyN5XXwUpl+O/HlNJeyteBQFaFapfBFMJ+g5fvsK2oqcV4tgHJEkWQTJi00UpW53rbR4VtI69b3xe5QwZsQzICCJk81HPs45tHklCsGlC8b7gUqMPYnCrtGFZIYmQZRr9HUSR2QtV0oXq62xULPNN9AK3YknDuctrVJaGfQLD5xEfmu48mbgcQXWIiuG8Q3sASu1KA4Wd+aDqvaiRglpl7yxrfaUpp1oZbfuADxLO4dvZFlBJ0sQ8jXkD5narAiElEx/3jb+Fe9QVi5VpTTTDt4JKnTPjJ5ex3m604q8TuQ1OhvO6G4/vkq8hn9m9PRalZDkWhd53EfdQ8w3wjAncDBiJu6Cr3gGSG3AWinsx36BKfDQhRrTC3+1dYYlMEyCnc34tWzORy/SZ/4AWkJFSSKR21a1hj26ZKSzvCMF5KLGJW10kHBH1xd0gKQFlBp6x6mCCDC/e5CIL8TzUe+E88Ggr7nFToDxWBeLq1SLVeK+Fdw6iSuDCmrAGrE+H3w67XC5CXb9QPna7qu4298jjNs/zQ2fRbxq1hwlffpXfIuVPgzH2/tTFYdBcolg+Qiw4BpnwNHRABCTtstg1qBBXw8DpD1Ahm2wdYTTMRah64eupp+pMXolKh5X9v7YtGOWEPkHbD68BWwukpCwScN0+nrYLN8ENlGYJh6cKHRd7LXAuX0T4CTuNcTmAqtqfBo4uaprLgsmeY1HraB0cg+KcDcFxiPXeRiPXZEREK3tNzhZ62wcQW06az2YPDgcOnaNvV2CMX4y2uEM/C+MRP+ejwNMoxmBehlG6dXwQwjPwuk0GWzMXs7U34QHPyTpGJpsosZrVy7sDuHK0X0nLc458HPjeHw9ADTu3vBJftZcGnd9JJ3BWDyJ5uWvaM5Oozk7L5rH1HQ7wn3txGkyi/af9I0we3vEbH4as/kZMYs9cdo3xUsiNsEZMjv7Mr0lMm+OyCxOI7M4IzKxOCc0/qfhJU24NIymk8mgK4/PndhuzC6PiIXTiIUzIjbyV11XpePwii69+BPhcva/JnM0/EHn/8Po/sO5/htQSwcII6bQxrkDAAD1EQAAUEsBAhQAFAAIAAgAYo9ePSOm0Ma5AwAA9REAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADzAwAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | |||
| + | Unter dem Inneren eines Vierecks <math>\overline {ABCD}</math> versteht man die Vereinigungsmenge des Inneren der Dreiecke <math>\overline {ABD}</math> und <math>\overline {BCD}</math>, wenn diese disjunkt sind (Skizze 1), sonst <math>\overline {ABC}</math> vereinigt mit <math>\overline {ACD}</math> (Skizze 2)--[[Benutzer:Andreas|Andreas]] 16:36, 30. Okt. 2010 (UTC) | ||
== Stufenwinkelsatz/Wechselwinkelsatz == | == Stufenwinkelsatz/Wechselwinkelsatz == | ||
Version vom 30. Oktober 2010, 17:36 Uhr
Inhaltsverzeichnis |
Spezielle Sinuswerte
Wie war das mit sin(30°)?
--*m.g.* 08:16, 15. Jul. 2010 (UTC): Versuchen Sie es mit einer Spiegelung an der x-Achse.
Kontrollfragen
Kann man mathematisch korrekt definieren: "Ein Viereck ist ein n-Eck mit n=4" oder ist das so nicht ausreichend?
Ist die Definition "Im Viereck ABCD sind die Winkel ABC, BCD, CDA und DAC Innenwinkel." eine mathematisch korrekte Definition von Innenwinkel eines Vierecks?
Definiert man "Inneres eines Vierecks/Dreiecks" über die Schnittmenge der vier bzw. drei Halbebenen (analog zum Inneren eines Winkels)?
Ich würde es so machen...
Unter dem Inneren eines Vierecks  versteht man die Vereinigungsmenge des Inneren der Dreiecke
versteht man die Vereinigungsmenge des Inneren der Dreiecke 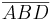 und
und 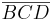 , wenn diese disjunkt sind (Skizze 1), sonst
, wenn diese disjunkt sind (Skizze 1), sonst  vereinigt mit
vereinigt mit 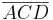 (Skizze 2)--Andreas 16:36, 30. Okt. 2010 (UTC)
(Skizze 2)--Andreas 16:36, 30. Okt. 2010 (UTC)
Stufenwinkelsatz/Wechselwinkelsatz
Kann man diese beiden Sätze auch ohne die Umkehrung beweisen?
Übungsserie 2, Beweis Satz 2.1 a)
Ich habe den Beweis ähnlich geführt wie in der Musterlösung. In der Musterlösung wurde mit der Zwischenrelation Zw (a,B,C) o.B.d.A. argumentiert, ich habe statt dessen mit der Kolliniarität koll (A,B,C) o.B.d.A. argumentiert. Ist das auch ok? Ansonsten war die Argumentation gleich.

