Diskussion:Quiz der Woche 2: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Definition: "Vierecksdiagonale") |
(→Definition: "Vierecksdiagonale") |
||
| Zeile 18: | Zeile 18: | ||
:: Es bleibt Ihnen natürlich unbenommen, sowas wie <math>\overline{AC}</math> als Diagonale nicht anzuerkennen. Sie müßten nur noch die Mathematiker überzeugen, sich von ihren diesbezüglichen üblichen Vorstellungen zu verabschieden. Verstehen Sie meine Bemerkungen um Himmels Willen nicht als Belehrungen. Konventionen lassen sich manchmal nicht begründen. Viel wichtiger ist Ihre Idee. | :: Es bleibt Ihnen natürlich unbenommen, sowas wie <math>\overline{AC}</math> als Diagonale nicht anzuerkennen. Sie müßten nur noch die Mathematiker überzeugen, sich von ihren diesbezüglichen üblichen Vorstellungen zu verabschieden. Verstehen Sie meine Bemerkungen um Himmels Willen nicht als Belehrungen. Konventionen lassen sich manchmal nicht begründen. Viel wichtiger ist Ihre Idee. | ||
| + | |||
| + | |||
| + | Wäre das ganze vllt. einfacher, wenn man den Eckpunkten des Vierecks einfach Namen gibt... also in etwa so: | ||
| + | In einem Viereck <math>\overline{ABCD}</math> nennt man die Strecken <math>\overline{AC}</math> und <math>\overline{BD}</math> Vierecksdiagonalen. --[[Benutzer:Andreas|Andreas]] 10:37, 29. Apr. 2010 (UTC) | ||
Version vom 29. April 2010, 11:37 Uhr
- Kann es sein, dass bei Frage 2 ("In welchen Fällen handelt es sich nicht um eine Definition?") das "nicht" zu viel ist? Laut Lösung müssen alle Antworten markiert werden, aber meiner Meinung nach und auch den Kommentaren nach handelt es sich bei allen Antworten um Definitionen (auch wenn sie nicht alle sinnvoll sind). Oder liege ich da falsch? --Ncesi1 11:16, 25. Apr. 2010 (UTC)
- Sie haben völlig Recht. In jedem Fall handelt es sich um eine Definition. Bin bei der Korrektur jedoch bei dem nicht geblieben, habe dafür die Bewertung der Antwort negiert. Vielen Dank für Ihre Aufmerksamkeit. --*m.g.* 11:36, 25. Apr. 2010 (UTC)
Definition: "Vierecksdiagonale"
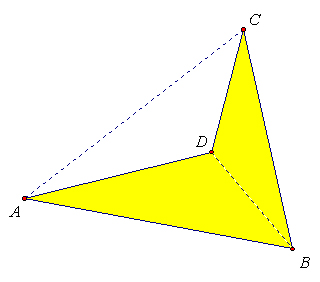
Hier eine Definition einer Vierecksdiagonalen, die ich für richtig halte: Eine Vierecksdiagonale ist eine Strecke, deren Endpunkte die Ecken eines Vierecks sind, die nicht zu ein und derselben Seite dieses Vierecks gehören und die offene Strecke komplett im Inneren des Vierecks liegt.--Andreas 13:34, 26. Apr. 2010 (UTC)
- was ist damit?
-
 ist eine Diagonale von
ist eine Diagonale von  --*m.g.* 15:31, 27. Apr. 2010 (UTC)
--*m.g.* 15:31, 27. Apr. 2010 (UTC)
Mit der Definition wollte ich die von ihnen gezeigte Diagonale  ausschließen. Ich hätte eine solche Strecke im ersten Moment nicht als Diagonale definiert. Aber ich lasse mich ja gerne belehren :) --Andreas 19:43, 27. Apr. 2010 (UTC)
ausschließen. Ich hätte eine solche Strecke im ersten Moment nicht als Diagonale definiert. Aber ich lasse mich ja gerne belehren :) --Andreas 19:43, 27. Apr. 2010 (UTC)
- Es bleibt Ihnen natürlich unbenommen, sowas wie
 als Diagonale nicht anzuerkennen. Sie müßten nur noch die Mathematiker überzeugen, sich von ihren diesbezüglichen üblichen Vorstellungen zu verabschieden. Verstehen Sie meine Bemerkungen um Himmels Willen nicht als Belehrungen. Konventionen lassen sich manchmal nicht begründen. Viel wichtiger ist Ihre Idee.
als Diagonale nicht anzuerkennen. Sie müßten nur noch die Mathematiker überzeugen, sich von ihren diesbezüglichen üblichen Vorstellungen zu verabschieden. Verstehen Sie meine Bemerkungen um Himmels Willen nicht als Belehrungen. Konventionen lassen sich manchmal nicht begründen. Viel wichtiger ist Ihre Idee.
- Es bleibt Ihnen natürlich unbenommen, sowas wie
Wäre das ganze vllt. einfacher, wenn man den Eckpunkten des Vierecks einfach Namen gibt... also in etwa so:
In einem Viereck  nennt man die Strecken
nennt man die Strecken  und
und 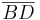 Vierecksdiagonalen. --Andreas 10:37, 29. Apr. 2010 (UTC)
Vierecksdiagonalen. --Andreas 10:37, 29. Apr. 2010 (UTC)

