Projektionen und Strahlensätze 2010: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Definition II.01: (Zentralprojektion des Ebene auf eine Gerade))
(→‎Definition II.01: (Zentralprojektion des Ebene auf eine Gerade))
Zeile 17: Zeile 17:
  
 
:: Es sei <math>\ g </math> eine Gerade der Ebene <math> \beta</math> und <math>\ Z</math> ein Punkt aus <math> \beta</math> der nicht zu <math>\ g </math> gehört.<br /> Die Zentralprojektion <math>\ ZP_{Z,g}</math> ist eine Abbildung von <math>\beta\setminus{Z}</math> auf die Gerade <math>\ g</math> mit:<br /><math>\forall P \in \beta\setminus{Z}: ZP_{Z,g}(P)=ZP \cap g</math>
 
:: Es sei <math>\ g </math> eine Gerade der Ebene <math> \beta</math> und <math>\ Z</math> ein Punkt aus <math> \beta</math> der nicht zu <math>\ g </math> gehört.<br /> Die Zentralprojektion <math>\ ZP_{Z,g}</math> ist eine Abbildung von <math>\beta\setminus{Z}</math> auf die Gerade <math>\ g</math> mit:<br /><math>\forall P \in \beta\setminus{Z}: ZP_{Z,g}(P)=ZP \cap g</math>
−
::Die Gerade <math>\ g </math> heißt Bildgerade bei der Zentralprojektion <math>\ ZP_{Z,g}</math> und der Punkt <math>\ Z</math> Zentralpunkt der <math>\ ZP_{Z,g}</math>.<br />
+
::Die Gerade <math>\ g </math> heißt Bildgerade bei der Zentralprojektion <math>\ ZP_{Z,g}</math> und der Punkt <math>\ Z</math> Zentralpunkt der <math>\ ZP_{Z,g}</math>.<br />--[[Benutzer:Tja???|Tja???]] 10:47, 13. Jan. 2011 (UTC)
  
  
 
[[Category:Elementargeometrie]]
 
[[Category:Elementargeometrie]]

Version vom 13. Januar 2011, 11:47 Uhr

Inhaltsverzeichnis

Zentralprojektionen

Wie kommt Lara Croft auf den Bildschirm?


Darstellung als Messung statt als Gaukelei: Holzschnitt von Albrecht Dürer, 1525

Zentralperspektive zeichnen.png Lochkamera prinzip.jpg

Begriff der Zentralprojektion

Definition II.01: (Zentralprojektion des Raumes auf eine Ebene)

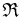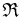Es sei \ \beta eine Ebene des Raumes \mathfrak{R} und \ Z ein Punkt aus \mathfrak{R} der nicht zu \ \beta gehört.
Die Zentralprojektion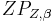 \ ZP_{Z,\beta} ist eine Abbildung von 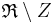\mathfrak{R}\setminus{Z} auf die Ebene \ \beta mit:
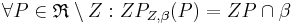
\forall P \in \mathfrak{R}\setminus{Z}: ZP_{Z,\beta}(P)=ZP \cap \beta
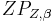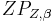Die Ebene \ \beta heißt Bildebene bei der Zentralprojektion \ ZP_{Z,\beta} und der Punkt \ Z Zentralpunkt der \ ZP_{Z,\beta}.

Definition II.01: (Zentralprojektion des Ebene auf eine Gerade)

Versuchen Sie es selbst.
Es sei \ g eine Gerade der Ebene \beta und \ Z ein Punkt aus \beta der nicht zu \ g gehört.
Die Zentralprojektion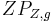 \ ZP_{Z,g} ist eine Abbildung von 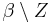\beta\setminus{Z} auf die Gerade \ g mit:
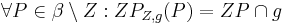
\forall P \in \beta\setminus{Z}: ZP_{Z,g}(P)=ZP \cap g
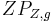Die Gerade \ g heißt Bildgerade bei der Zentralprojektion \ ZP_{Z,g} und der Punkt \ Z Zentralpunkt der \ ZP_{Z,g}.
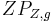--Tja??? 10:47, 13. Jan. 2011 (UTC)
Von „http://geometrie.zum.de/index.php?title=Projektionen_und_Strahlensätze_2010&oldid=5948“