Die Umkehrung des Stufenwinkelsatzes (WS10/11): Unterschied zwischen den Versionen
(→Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)) |
(→Definition X.3: (entgegengesetzt liegende Winkel)) |
||
| Zeile 16: | Zeile 16: | ||
Übungsaufgabe | Übungsaufgabe | ||
| + | |||
| + | Wenn zwei zueinander parallele Geraden p und p* von einer Geraden g geschnitten werden, so bezeichnet man die beiden Winkel <gp und <gp*, die bezüglich der Geraden g in derselben Halbebene, aber jeweils auf unterschiedlichen Seiten von p und p* liegen, als entgegengesetzt liegende Winkel. Entgegengesetzt liegende Winkel ergänzen sich zu 180°(diese Eigenschaft folgt direkt aus dem Parallelenaxiom der euklidischen Geometrie).(Umgekehrt kann auf die Parallelität von Geraden geschlossen werden)--[[Benutzer:Halikarnaz|Halikarnaz]] 13:22, 23. Jan. 2011 (UTC) | ||
== Die Umkehrung des Stufenwinkelsatzes == | == Die Umkehrung des Stufenwinkelsatzes == | ||
Version vom 23. Januar 2011, 14:22 Uhr
Inhaltsverzeichnis |
Stufenwinkel, Wechselwinkel, entgegengesetzt liegende Winkel
In welchen Fällen handelt es sich um....
- Stufenwinkel
- Wechselwinkel
- entgegengesetzt liegende Winkel?
Definition X.1: (Stufenwinkel)
Definition X.2: (Wechselwinkel)
Definition X.3: (entgegengesetzt liegende Winkel)
Übungsaufgabe
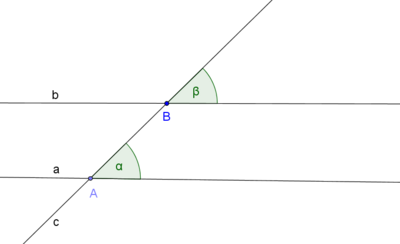
Wenn zwei zueinander parallele Geraden p und p* von einer Geraden g geschnitten werden, so bezeichnet man die beiden Winkel <gp und <gp*, die bezüglich der Geraden g in derselben Halbebene, aber jeweils auf unterschiedlichen Seiten von p und p* liegen, als entgegengesetzt liegende Winkel. Entgegengesetzt liegende Winkel ergänzen sich zu 180°(diese Eigenschaft folgt direkt aus dem Parallelenaxiom der euklidischen Geometrie).(Umgekehrt kann auf die Parallelität von Geraden geschlossen werden)--Halikarnaz 13:22, 23. Jan. 2011 (UTC)
Die Umkehrung des Stufenwinkelsatzes
Satz X.1: (Umkehrung des Stufenwinkelsatzes)
- Es seien
 und
und  zwei nicht identische Geraden, die durch eine dritte Gerade
zwei nicht identische Geraden, die durch eine dritte Gerade  jeweils geschnitten werden. Es seien ferner
jeweils geschnitten werden. Es seien ferner  und
und  zwei Stufenwinkel, die bei dem Schnitt von
zwei Stufenwinkel, die bei dem Schnitt von  mit
mit  und
und  entstehen mögen.
entstehen mögen.
- Wenn die beiden Stufenwinkel
 und
und  kongruent zueinander sind, dann sind die Geraden
kongruent zueinander sind, dann sind die Geraden  und
und  parallel zueinander.
parallel zueinander.
- Es seien
Beweis von Satz X.1: (Umkehrung des Stufenwinkelsatzes)
Es seien 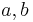 und
und  drei paarweise nicht identische Geraden. Die Gerade
drei paarweise nicht identische Geraden. Die Gerade  möge
möge  in dem Punkt
in dem Punkt und die Gerade
und die Gerade  in dem Punkt
in dem Punkt  schneiden.
schneiden.  und
und  sei ein Paar von Stufenwinkeln , welches bei dem Schnitt von
sei ein Paar von Stufenwinkeln , welches bei dem Schnitt von  und
und  mit
mit  entstehen möge.
entstehen möge.
Voraussetzung:
(i) 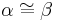
Behauptung:
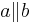
Annahme:
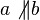
Den Rest können Sie selbst!
Voraussetzung:
-
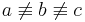
-
 und
und  sind Stufenwinkel
sind Stufenwinkel
-
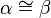
-
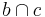 = {
= { }
}
-
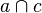 = {
= { }
}
Behauptung:
Annahme:
1) 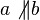
|
Annahme |
2) 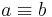 oder oder 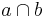 = { = { } }
|
1), Schnittpunkt von Geraden |
3) 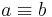
|
Widerspruch zur 1. Voraussetzung |
4) 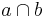 = { = { } }  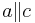 oder oder 
|
2), Definition Schnittpunkt von Geraden, 2. und 3. Voraussetzung |
5) 
|
Widerspruch zur 1. und 5. Voraussetzung |
6) 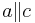
|
Widerspruch zur 5. Voraussetzung |
 Annahme verwerfen
Annahme verwerfen  Behauptung stimmt.
Behauptung stimmt.
q.e.d.--Jbo-sax 18:39, 20. Jan. 2011 (UTC)