Peripheriewinkelsatz und Zentriwinkel-Peripheriewinkelsatz (WS10/11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
TimoRR (Diskussion | Beiträge) (→Definition XIX.1 (Peripheriewinkel)) |
TimoRR (Diskussion | Beiträge) (→Definition XIX.2 (Zentriwinkel)) |
||
| Zeile 12: | Zeile 12: | ||
Gegeben sei ein Kreis k, M der Mittelpunkt von k und die Punkte <math>A,B \in k</math>.<br /> | Gegeben sei ein Kreis k, M der Mittelpunkt von k und die Punkte <math>A,B \in k</math>.<br /> | ||
| − | Ein Zentriwinkel ist ein Winkel, dessen Scheitel in M liegt und dessen Schenkel durch A und B verlaufen.--[[Benutzer:Engel82|Engel82]] 13:20, 30. Jan. 2011 (UTC) | + | Ein Zentriwinkel ist ein Winkel, dessen Scheitel in M liegt und dessen Schenkel durch A und B verlaufen.--[[Benutzer:Engel82|Engel82]] 13:20, 30. Jan. 2011 (UTC)<br /> |
| + | Ein Zentriwinkel ist ein Winkel, dessen Scheitelpunkt der Mittelpunkt eines Kreises ist und dessen Schenkel den Kreis in jeweils einem Punkt schneiden.--[[Benutzer:TimoRR|TimoRR]] 12:57, 5. Feb. 2011 (UTC) | ||
<ggb_applet width="466" height="399" version="3.2" ggbBase64="UEsDBBQACAAIADGnPT4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vnbcts2EH1uvoLDd9G4g5yRkpHd6Uxm4qYTp3noG0VCEmqKVEnIlvxXmf5Hv6kLgNTVUa04dSK/0FxAi8U5e3YBqf9mOSuCO1U3uioHIY5QGKgyq3JdTgbhwox7cfjm9av+RFUTNarTYFzVs9QMQhqR0NoX+vWrn/rNtLoP0sJN+aTV/SAcp0WjwqCZ1yrNm6lSZseeLpa60Gm9ej/6U2Wm2Qx4J2/L+QJWMfUCbNksf6eb7vXCLTgvtPlZ3+lc1UFRZYNQcAgd/vukaqOztBiEDHkLGYRkbxBM1I5Oq1o/VKWx0zfOx2AJgkY/KECEWFv/wm20rxZZoXOdlnYzLg6YFAT3OjdTWFAIcKn0ZGoBSqT3llVVnd+sGqNmwfIPVVeDUDKL88q/UOxQbyAsWI8jN7T95ryouxtlDLDSBOlSbfCa1DrfeXnbXFbFxjSvdGmu0rlZ1I5S2ppuzMouAGvVNt5hOSlUayOA+FRlt6NqeeMxoN71x9XcfcQFNJpcVUVVB7VFl8OE9jnyTzfHRrqehdwc5Ga0PqzT9ThOiJvhniP/dLMKXfrQ2p3jbtcYdcvoJrAGCyNk4nrzRTpSwGwYLEpt3nUvkAG37Vax/8Cvi9kIJLCdA2uf+Fv57F/sZU//VtWlKnyOlMDtolo0wZ3NRb+WCyRXmZ7Bqx9oIUktXb9DAN6aq0mtusC9gDxgbhRt5+GeuX/RBWFjaCDWzEAlgP0YuxcrVAMiGYQ32bTUdTYNgzw1dsSqoVAzBVIxLi9cWq3xuQ7XdaFyEu/E3I5vkIbhR3PEZVNazKcpWDoZFOkKBL+9Lefvusp3N5uWAJrbCehubh1YWuZKeUZNm8nBHBw6XWwh7oBqgqUtcgy0aMtiAsp+8PXRzfEasuJ3q9KWYA/If0DzyyE0u7l1FtiQCHlwWMTIaeBk1WyWlnlQpjNY6QrSqlAOE22rfpAimz5Bii1UHoaF6QZuvbPWxQHSkMQ6WwN5G+7WDzMFmZaqaVyRM9vl7DmZip7MxfvxuFHGwtejxKHXw+QYV0+KHTqOKu8g8qpugmCJ2j6+Qj6g4KGzLAHSnm8wuDU94C3iIC1qvQyG3fxhN2sIDVNGHCGabP7ATNsVhszuyKplyO2erF58aH+VPvzGF0dIs0yPgaKjKfGb08tuRtwepMLV8VTYFd3VV9UjTHxnc88fQ3dw8OIsRoQynCDCqZCtCqWQmDNJKMFSEPocST4N/+Ep+A9fHP8treHEYfQC7KBIYoISnsQCJQQL3DUQTCWPsUBSxCzBLP7/6bk8hZ7L70iP8BC9ADs8igF/IAdkgyRBiPu8iAQFzihhCYlpwixpX8/Oh3S1x82Vb2bDA4rS4xTV4KkjIP0WrWwLlOf3sgOOtmuUIAmXcLPhgKpEsVdBj0ScwaugHLSAQBG+SqGIIplQzCl8hHEOVeyU7rfXYvQM7oaZNmu0C5sRb0sDp3HlTreHh+xbpeb2dvO+/FinZWMvuX7O1uH9VLovD+gePZ3u0TnRzaC6CYIwkzShVMTYsU0gCQjikmMsEVyNvah6hMPhgBBpqyTDmODzodpdkvfIHnqyLefkMc7/+fs46e4mt2YMZtvPQzyLFmzoHBJaCUoEjyVlnJDnnFcxOqQdP5H2U4hK62yrXnbGoqjuP6hxoZYOyafCfqMm1v448IeIZ8cBb1pvHVzZOSkNwRlcCGhSPGYIJZAQTmo8woJJQWMBauNwSPdSExGhAkP1RQzLGHR4PlI7yvn1Aef5aZzn58Q5XNhiQhiGkwmBHoliTrr6GssEMYRpgmRMY94W2AguAUhAJaY0jpFk58769ZeUrk5jXZ0T6ziiBMgFQSMJ1wYei5Z0tnuC9d9L9ZIIzk6gcyI4R0zig69Of1zSj3TV6y921c8nddXP+12VRJQTHGM4dEomAGf2sl11c/nxt/ce/d4t92L761/3g0f7i8/rfwFQSwcIHuZo3L0FAAAjGgAAUEsBAhQAFAAIAAgAMac9Ph7maNy9BQAAIxoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAD3BQAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="466" height="399" version="3.2" ggbBase64="UEsDBBQACAAIADGnPT4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vnbcts2EH1uvoLDd9G4g5yRkpHd6Uxm4qYTp3noG0VCEmqKVEnIlvxXmf5Hv6kLgNTVUa04dSK/0FxAi8U5e3YBqf9mOSuCO1U3uioHIY5QGKgyq3JdTgbhwox7cfjm9av+RFUTNarTYFzVs9QMQhqR0NoX+vWrn/rNtLoP0sJN+aTV/SAcp0WjwqCZ1yrNm6lSZseeLpa60Gm9ej/6U2Wm2Qx4J2/L+QJWMfUCbNksf6eb7vXCLTgvtPlZ3+lc1UFRZYNQcAgd/vukaqOztBiEDHkLGYRkbxBM1I5Oq1o/VKWx0zfOx2AJgkY/KECEWFv/wm20rxZZoXOdlnYzLg6YFAT3OjdTWFAIcKn0ZGoBSqT3llVVnd+sGqNmwfIPVVeDUDKL88q/UOxQbyAsWI8jN7T95ryouxtlDLDSBOlSbfCa1DrfeXnbXFbFxjSvdGmu0rlZ1I5S2ppuzMouAGvVNt5hOSlUayOA+FRlt6NqeeMxoN71x9XcfcQFNJpcVUVVB7VFl8OE9jnyTzfHRrqehdwc5Ga0PqzT9ThOiJvhniP/dLMKXfrQ2p3jbtcYdcvoJrAGCyNk4nrzRTpSwGwYLEpt3nUvkAG37Vax/8Cvi9kIJLCdA2uf+Fv57F/sZU//VtWlKnyOlMDtolo0wZ3NRb+WCyRXmZ7Bqx9oIUktXb9DAN6aq0mtusC9gDxgbhRt5+GeuX/RBWFjaCDWzEAlgP0YuxcrVAMiGYQ32bTUdTYNgzw1dsSqoVAzBVIxLi9cWq3xuQ7XdaFyEu/E3I5vkIbhR3PEZVNazKcpWDoZFOkKBL+9Lefvusp3N5uWAJrbCehubh1YWuZKeUZNm8nBHBw6XWwh7oBqgqUtcgy0aMtiAsp+8PXRzfEasuJ3q9KWYA/If0DzyyE0u7l1FtiQCHlwWMTIaeBk1WyWlnlQpjNY6QrSqlAOE22rfpAimz5Bii1UHoaF6QZuvbPWxQHSkMQ6WwN5G+7WDzMFmZaqaVyRM9vl7DmZip7MxfvxuFHGwtejxKHXw+QYV0+KHTqOKu8g8qpugmCJ2j6+Qj6g4KGzLAHSnm8wuDU94C3iIC1qvQyG3fxhN2sIDVNGHCGabP7ATNsVhszuyKplyO2erF58aH+VPvzGF0dIs0yPgaKjKfGb08tuRtwepMLV8VTYFd3VV9UjTHxnc88fQ3dw8OIsRoQynCDCqZCtCqWQmDNJKMFSEPocST4N/+Ep+A9fHP8treHEYfQC7KBIYoISnsQCJQQL3DUQTCWPsUBSxCzBLP7/6bk8hZ7L70iP8BC9ADs8igF/IAdkgyRBiPu8iAQFzihhCYlpwixpX8/Oh3S1x82Vb2bDA4rS4xTV4KkjIP0WrWwLlOf3sgOOtmuUIAmXcLPhgKpEsVdBj0ScwaugHLSAQBG+SqGIIplQzCl8hHEOVeyU7rfXYvQM7oaZNmu0C5sRb0sDp3HlTreHh+xbpeb2dvO+/FinZWMvuX7O1uH9VLovD+gePZ3u0TnRzaC6CYIwkzShVMTYsU0gCQjikmMsEVyNvah6hMPhgBBpqyTDmODzodpdkvfIHnqyLefkMc7/+fs46e4mt2YMZtvPQzyLFmzoHBJaCUoEjyVlnJDnnFcxOqQdP5H2U4hK62yrXnbGoqjuP6hxoZYOyafCfqMm1v448IeIZ8cBb1pvHVzZOSkNwRlcCGhSPGYIJZAQTmo8woJJQWMBauNwSPdSExGhAkP1RQzLGHR4PlI7yvn1Aef5aZzn58Q5XNhiQhiGkwmBHoliTrr6GssEMYRpgmRMY94W2AguAUhAJaY0jpFk58769ZeUrk5jXZ0T6ziiBMgFQSMJ1wYei5Z0tnuC9d9L9ZIIzk6gcyI4R0zig69Of1zSj3TV6y921c8nddXP+12VRJQTHGM4dEomAGf2sl11c/nxt/ce/d4t92L761/3g0f7i8/rfwFQSwcIHuZo3L0FAAAjGgAAUEsBAhQAFAAIAAgAMac9Ph7maNy9BQAAIxoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAD3BQAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
Version vom 5. Februar 2011, 13:57 Uhr
Inhaltsverzeichnis |
Definition XIX.1 (Peripheriewinkel)
Der Winkel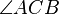 
im nachfolgenden Applet ist ein Peripheriewinkel. Definieren Sie diesen Begriff:
Gegeben sei ein Kreis k und die Punkte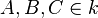 
.
Ein Peripheriewinkel ist ein Winkel, dessen Scheitel in C liegt und dessen Schenkel durch A und B verlaufen.--Engel82 13:17, 30. Jan. 2011 (UTC)
Ein Peripheriewinkel ist ein Winkel, dessen Scheitelpunkt Element eines Kreises ist und dessen Schenkel den Kreis in jeweils einem Punkt schneiden.--TimoRR 12:57, 5. Feb. 2011 (UTC)
Definition XIX.2 (Zentriwinkel)
Der Winkel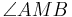 
im nachfolgenden Applet ist ein Zentriwinkel. Definieren Sie diesen Begriff:
Gegeben sei ein Kreis k, M der Mittelpunkt von k und die Punkte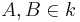 
.
Ein Zentriwinkel ist ein Winkel, dessen Scheitel in M liegt und dessen Schenkel durch A und B verlaufen.--Engel82 13:20, 30. Jan. 2011 (UTC)
Ein Zentriwinkel ist ein Winkel, dessen Scheitelpunkt der Mittelpunkt eines Kreises ist und dessen Schenkel den Kreis in jeweils einem Punkt schneiden.--TimoRR 12:57, 5. Feb. 2011 (UTC)
Idee des Beweises eines Spezialfalls
Um welchen Spezialfall handelt es sich?
Können Sie einen formalen Beweis aus dem Video ableiten?
Der Zentri-Peripheriewinkelsatz
ergänzen Sie: Jeder Peripheriewinkel ist halb so groß wie sein zugehöriger Zentriwinkel.--Engel82 13:22, 30. Jan. 2011 (UTC)
Satz XIX.1:(Der Zentri-Peripheriewinkelsatz)
Der Peripheriewinkelsatz
Satz XIX.2:(Der Peripheriewinkelsatz)
ergänzen Sie: Alle Peripheriewinkel über derselben Sehne sind kongruent zueinander.--Engel82 13:23, 30. Jan. 2011 (UTC)
