Lösung von Aufgabe 2.7 (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 2: | Zeile 2: | ||
| − | Gegeben sei ein Winkel BAC und der Strahl AP<sup>+</sup> der im Inneren des Winkels BAC liegt. Die WH des Winkels BAC ist der Strahl AP<sup>+</sup> der den Winkel BAC in zwei gleich große Winkel einteilt. In Winkel PAC und PAB.--[[Benutzer:Celebino|Celebino]] 09:22, 20. Apr. 2011 (CEST)<br /> | + | Gegeben sei ein Winkel <math>\angle {BAC}</math> und der Strahl AP<sup>+</sup> der im Inneren des Winkels <math>\angle {BAC}</math> liegt. Die WH des Winkels <math>\angle {BAC}</math> ist der Strahl AP<sup>+</sup>, der den Winkel <math>\angle {BAC}</math> in zwei gleich große Winkel einteilt. In Winkel <math>\angle {PAC}</math> und <math>\angle {PAB}</math> .--[[Benutzer:Celebino|Celebino]] 09:22, 20. Apr. 2011 (CEST)<br /> |
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 20. April 2011, 09:38 Uhr
Geben Sie eine exakte Definition des Begriffs Winkelhalbierende an (orientieren Sie sich gegebenenfalls an Schulbuchdefinitionen). Notieren Sie, welche anderen Begriffe Sie dazu verwenden.
Gegeben sei ein Winkel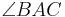 
und der Strahl AP+ der im Inneren des Winkels 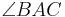liegt. Die WH des Winkels 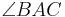ist der Strahl AP+, der den Winkel 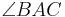in zwei gleich große Winkel einteilt. In Winkel 
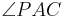und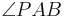 
.--Celebino 09:22, 20. Apr. 2011 (CEST)
