Lösung von Aufg. 7.3 (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“. | Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“. | ||
| + | <br\><br\> | ||
| + | Definition komplanar:<br\> | ||
Eine Menge von Punkten <math>M = \{ P_1, P_2, ..., P_n, ..\}</math> heißt komplanar genau dann, wenn eine Ebene E exisitert mit <math>M \subseteq E</math>--[[Benutzer:Peterpummel|Peterpummel]] 12:22, 23. Mai 2011 (CEST) | Eine Menge von Punkten <math>M = \{ P_1, P_2, ..., P_n, ..\}</math> heißt komplanar genau dann, wenn eine Ebene E exisitert mit <math>M \subseteq E</math>--[[Benutzer:Peterpummel|Peterpummel]] 12:22, 23. Mai 2011 (CEST) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 23. Mai 2011, 11:23 Uhr
Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“.
Definition komplanar:
Eine Menge von Punkten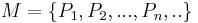 
heißt komplanar genau dann, wenn eine Ebene E exisitert mit 
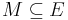--Peterpummel 12:22, 23. Mai 2011 (CEST)
